Pertanyaan

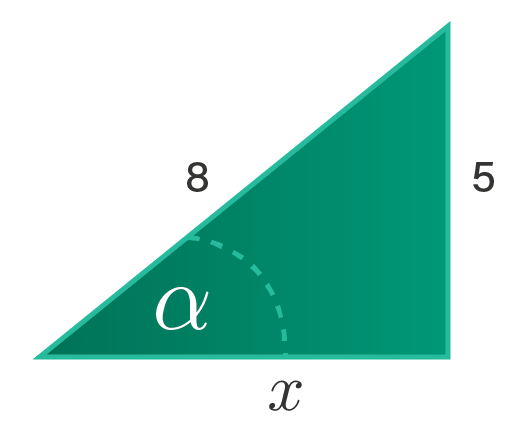
Sebuah bak penampung air diperlihatkan pada gambar berikut. Pada sisi kanan bak dibuat saluran air pada ketinggian 10 m dari atas tanah dengan sudut kemiringan α °. Jika kecepatan gravitasi bumi 10 m/s 2 tentukan: a) kecepatan keluarnya air. b) waktu yang diperlukan untuk sampai ke tanah. c) nilai cos α d) perkiraan jarak jatuh air pertama kali ( d ) saat saluran dibuka. (Gunakan sin α = 5/8 dan 39 = 6 , 24 )

Sebuah bak penampung air diperlihatkan pada gambar berikut. Pada sisi kanan bak dibuat saluran air pada ketinggian 10 m dari atas tanah dengan sudut kemiringan α°.

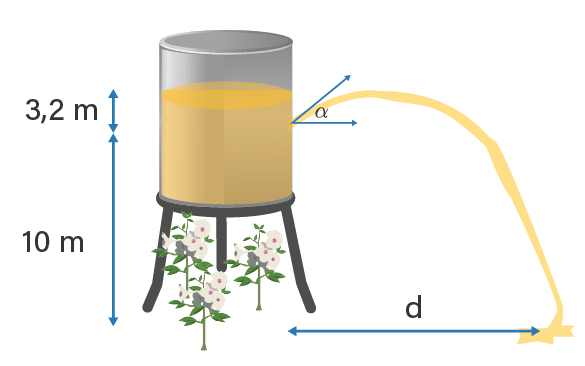
Jika kecepatan gravitasi bumi 10 m/s² tentukan:

a) kecepatan keluarnya air.

b) waktu yang diperlukan untuk sampai ke tanah.

c) nilai cos α

d) perkiraan jarak jatuh air pertama kali (d) saat saluran dibuka.

(Gunakan $sin α = 5/8$ dan $39 = 6, 24$ )

J. Khairina

Master Teacher

Mahasiswa/Alumni Universitas Pendidikan Indonesia

Jawaban terverifikasi

Jawaban

maka kecepatankeluarnya air adalah 8 m/s,waktu yang diperlukan untuk sampai ke tanah adalah 2 s,nilaicos α adalah 0,78, danjarak jatuh air pertama kalisaat saluran dibuka aalah 12,48 m.

maka kecepatan keluarnya air adalah 8 m/s, waktu yang diperlukan untuk sampai ke tanah adalah 2 s, nilai cos α adalah 0,78, dan jarak jatuh air pertama kali saat saluran dibuka aalah 12,48 m.

Pembahasan

Diketahui h 1 = 3 , 2 m h 2 = 10 m g = 10 m / s 2 sin α = 5/8 Ditanyakan a) kecepatan keluarnya air b) waktu yang diperlukan untuk sampai ke tanah c) nilai cos α d) perkiraan jarak jatuh air pertama kali ( d ) saat saluran dibuka Jawab Pada tangki yang berlubang, berlaku Teorema Torricelli yang merupakan turunan dari Hukum Bernoulli . Teorema Torricelli menyatakan bahwa " Kecepatan semburan air melalui lubang dengan jarak h dari permukaan air sama dengan kecepatan jatuh bebas air dari ketinggianh" . a) kecepatan keluarnya air Dengan menggunakan rumus dari Hukum Bernoulli , kecepatan keluarnya air dapat dihitung menggunakan rumus berikut: P 1 + ρ g h 1 + 2 1 ρ v 1 2 P 0 + ρ g h 1 + 0 ρ g ( h 1 − h 2 ) v 2 2 v 2 = = = = = P 2 + ρ g h 2 + 2 1 ρ v 2 2 P 0 + ρ g h 2 + 2 1 ρ v 2 2 2 1 ρ v 2 2 2 g h 2 g h Keterangan: P 0 = tekanan pada ujung pipa (Pa) ρ = massa jenis fluida (kg/m 3 ) v = kecepatan aliran fluida (m/s) g = percepatan gravitasi (m/s 2 ) h = ketinggian (m) Berdasarkan rumus di atas, maka kecepatan keluarnya air adalah: v = 2 g h 1 v = 2 ( 10 ) ( 3 , 2 ) v = 64 v = 8 m / s Jadi, kecepatan keluarnya air adalah 8 m/s. b) waktu yang diperlukan untuk sampai ke tanah Untuk menghitung waktu saat mencapai tanah, gunakan persamaan dari gerak parabola. Karena air bergerak turun ke bawah dari ketinggian h 2 = 10 m, maka nilai y = − 10 m . (tanda (-) menunjukkan arah ke bawah). y − 10 − 10 5 t 2 − 5 t − 10 t 2 − t − 2 ( t − 2 ) ( t + 1 ) = = = = = = ( v 0 sin α ) t − 2 1 g t 2 8 ( 8 5 ) t − 2 1 ( 10 ) t 2 5 t − 5 t 2 0 0 0 Dengan demikian maka nilai t adalah t = 2 s atau t = -1 s. Nilai yang dipilih adalah 2 s karena waktu tidak dapat bernilai negatif. Jadi, waktu yang diperlukan untuk sampai ke tanah adalah 2 s. c) nilai cos α Nialai sin α telah diketahui yaitu 5/8, maka nilai cos α adalah: cos α = 8 x cos α = 8 8 2 − 5 2 cos α = 8 39 cos α = 8 6 , 24 cos α = 0 , 78 Jadi, nilaicos α adalah 0,78. d) perkiraan jarak jatuh air pertama kali ( d ) saat saluran dibuka Jarak mendatar jatuhnya air dhitung menggunakan rumus berikut. d = ( v 0 cos α ) t d = 8 ( 8 39 ) 2 d = 2 ( 6 , 24 ) d = 12 , 48 m Jadi,perkiraan jarak jatuh air pertama kalisaat saluran dibuka aalah 12,48 m. Dengan demikian, maka kecepatankeluarnya air adalah 8 m/s,waktu yang diperlukan untuk sampai ke tanah adalah 2 s,nilaicos α adalah 0,78, danjarak jatuh air pertama kalisaat saluran dibuka aalah 12,48 m.

Diketahui

$h_{1} = 3, 2 m h_{2} = 10 m g = 10 m / s^{2} sin α = 5/8$

Ditanyakan

a) kecepatan keluarnya air

b) waktu yang diperlukan untuk sampai ke tanah

c) nilai cos α

d) perkiraan jarak jatuh air pertama kali (d) saat saluran dibuka

Jawab

Pada tangki yang berlubang, berlaku Teorema Torricelli yang merupakan turunan dari Hukum Bernoulli. Teorema Torricelli menyatakan bahwa "Kecepatan semburan air melalui lubang dengan jarak h dari permukaan air sama dengan kecepatan jatuh bebas air dari ketinggian h" .

a) kecepatan keluarnya air

Dengan menggunakan rumus dari Hukum Bernoulli, kecepatan keluarnya air dapat dihitung menggunakan rumus berikut:

$P_{1} + ρ g h_{1} + \frac{1}{2} ρ v_{1}^{2} P_{0} + ρ g h_{1} + 0 ρ g (h_{1} - h_{2}) v_{2}^{2} v_{2} = = = = = P_{2} + ρ g h_{2} + \frac{1}{2} ρ v_{2}^{2} P_{0} + ρ g h_{2} + \frac{1}{2} ρ v_{2}^{2} \frac{1}{2} ρ v_{2}^{2} 2 g h 2 g h$

Keterangan:

$P_{0}$ = tekanan pada ujung pipa (Pa)
$ρ$ = massa jenis fluida (kg/m³)
$v$ = kecepatan aliran fluida (m/s)
$g$ = percepatan gravitasi (m/s²)
$h$ = ketinggian (m)

Berdasarkan rumus di atas, maka kecepatan keluarnya air adalah:

$v = 2 g h_{1} v = 2 (10) (3, 2) v = 64 v = 8 m / s$

Jadi, kecepatan keluarnya air adalah 8 m/s.

b) waktu yang diperlukan untuk sampai ke tanah

Untuk menghitung waktu saat mencapai tanah, gunakan persamaan dari gerak parabola. Karena air bergerak turun ke bawah dari ketinggian h₂ = 10 m, maka nilai $y = - 10 m$ . (tanda (-) menunjukkan arah ke bawah).

$y - 10 - 10 5 t^{2} - 5 t - 10 t^{2} - t - 2 (t - 2) (t + 1) = = = = = = (v_{0} sin α) t - \frac{1}{2} g t^{2} 8 (\frac{5}{8}) t - \frac{1}{2} (10) t^{2} 5 t - 5 t^{2} 000$

Dengan demikian maka nilai t adalah t = 2 s atau t = -1 s. Nilai yang dipilih adalah 2 s karena waktu tidak dapat bernilai negatif.

Jadi, waktu yang diperlukan untuk sampai ke tanah adalah 2 s.

c) nilai cos α

Nialai sin α telah diketahui yaitu 5/8, maka nilai cos α adalah:

$cos α = \frac{x}{8} cos α = \frac{8 ^{2} - 5 ^{2}}{8} cos α = \frac{39}{8} cos α = \frac{6 , 24}{8} cos α = 0, 78$

Jadi, nilai cos α adalah 0,78.

d) perkiraan jarak jatuh air pertama kali (d) saat saluran dibuka

Jarak mendatar jatuhnya air dhitung menggunakan rumus berikut.

$d = (v_{0} cos α) t d = 8 (\frac{39}{8}) 2 d = 2 (6, 24) d = 12, 48 m$

Jadi, perkiraan jarak jatuh air pertama kali saat saluran dibuka aalah 12,48 m.

Dengan demikian, maka kecepatan keluarnya air adalah 8 m/s, waktu yang diperlukan untuk sampai ke tanah adalah 2 s, nilai cos α adalah 0,78, dan jarak jatuh air pertama kali saat saluran dibuka aalah 12,48 m.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.7 (7 rating)

Tuti Handayani

Mudah dimengerti

Pertanyaan serupa

Dalam percobaan Torricelli, terdapat ruang hampa dalam tabung itu, sedangkan bagian yang lainnya berisi raksa. Dalam kasus ini:

5.0

Jawaban terverifikasi

Sebuah tabung berisi penuh zat cair (ideal). Pada dindingnya sejauh 20 cm dari permukaan atas terdapat lubang kecil (jauh lebih kecil dari penampang tabung) sehingga zat cair memancar (terlihat sepert...

4.8

Jawaban terverifikasi

Sebuah tangki air bocor memiliki 2 lubang seperti pada gambar berikut. Perbandingan jarak mendatar pancaran air dari lubang Adan lubang Badalah ....

5.0

Jawaban terverifikasi

Sebuah tabung berisi zat cair (ideal). Pada dindingnya terdapat dua lubang kecil (jauh lebih kecil dari penampang tabung) sehingga zat cair memancar (terlihat seperti pada gambar). Perbanding...

363

4.8

Jawaban terverifikasi

Fluida mengalir melalui iubang kecil pada dinding bak (lihat gambar). Perbandingan x 1 : x 2 adalah ....

0.0

Jawaban terverifikasi