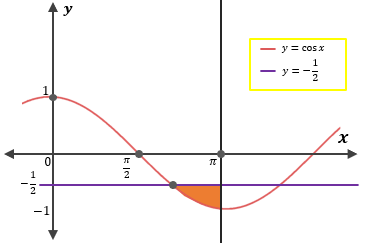
Akan digunakan dua metode, yaitu metode grafik dan metode garis bilangan.
Metode Grafik
Untuk menentukan pertidaksamaan yang tepat, akan dicari titik potong antara  dan
dan  dengan cara sebagai berikut.
dengan cara sebagai berikut.

Nilai x yang memenuhi  adalah
adalah  dan seterusnya. Namun, perhatikan bahwa daerah tersebut berada pada interval
dan seterusnya. Namun, perhatikan bahwa daerah tersebut berada pada interval  sehingga nilai x yang memenuhi adalah
sehingga nilai x yang memenuhi adalah  . Untuk lebih jelasnya, perhatikan gambar berikut!
. Untuk lebih jelasnya, perhatikan gambar berikut!
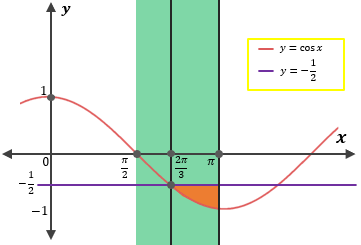
Dengan demikian, himpunan penyelesaian dari daerah yang berwarna adalah  .
.
Metode Garis Bilangan
Sebelumnya, perhatikan bahwa daerah terebut berada pada interval  .
.
Kemudian, perhatikan bahwa daerah teresebut dibatas dengan garis  berada di atas sementara kurva
berada di atas sementara kurva  berada di bawah. Artinya, pertidaksamaannya adalah
berada di bawah. Artinya, pertidaksamaannya adalah  .
.
Kemudian, perhatikan bahwa

Ruas kiri akan menjadi nol jika  sehingga didapat perhitungan sebagai berikut.
sehingga didapat perhitungan sebagai berikut.

Akibatnya, didapat  atau
atau  .
.
Dengan kata lain, didapat dua hasil sebagai berikut.

atau

dengan k dan p adalah bilangan bulat.
Akan dibagi menjadi dua kasus.
- Kasus I:
 atau
atau 
Perhatikan jika k = 0, maka didapat  atau
atau  yang keduanya tidak memenuhi syarat
yang keduanya tidak memenuhi syarat  . Akibatnya, k = 0 tidak memenuhi dan untuk nilai k yang lebih besar juga pasti tidak memenuhi.
. Akibatnya, k = 0 tidak memenuhi dan untuk nilai k yang lebih besar juga pasti tidak memenuhi.
Kemudian, perhatikan jika  , maka didapat
, maka didapat  atau
atau  yang keduanya juga tidak memenuhi syarat
yang keduanya juga tidak memenuhi syarat  . Akibatnya,
. Akibatnya,  tidak memenuhi dan untuk nilai k yang lebih kecil juga pasti tidak memenuhi.
tidak memenuhi dan untuk nilai k yang lebih kecil juga pasti tidak memenuhi.
Dengan demikian, untuk kasus I tidak ada penyelesaian yang memenuhi.
- Kasus II:
 atau
atau 
Perhatikan jika p = 0, maka didapat  atau
atau  . Karena yang memenuhi syarat
. Karena yang memenuhi syarat  adalah
adalah  saja, maka diambil
saja, maka diambil  sebagai penyelesaian.
sebagai penyelesaian.
Kemudian, jika p = 1, didapat  atau
atau  yang keduanya tidak memenuhi syarat
yang keduanya tidak memenuhi syarat  . Akibatnya, p = 1 tidak memenuhi dan untuk nilai p yang lebih besar juga pasti tidak memenuhi.
. Akibatnya, p = 1 tidak memenuhi dan untuk nilai p yang lebih besar juga pasti tidak memenuhi.
Lalu, jika  , didapat
, didapat  atau
atau  yang keduanya juga tidak memenuhi syarat
yang keduanya juga tidak memenuhi syarat  . Akibatnya,
. Akibatnya,  tidak memenuhi dan untuk nilai p yang lebih kecil juga pasti tidak memenuhi.
tidak memenuhi dan untuk nilai p yang lebih kecil juga pasti tidak memenuhi.
Dengan demikian, dari kasus II didapat solusinya adalah  .
.
Akibatnya, diperoleh garis bilangan sebagai berikut.
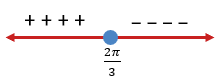
Karena tanda pertidaksamaannya adalah ≤, maka diambil  . Namun, karena syaratnya adalah
. Namun, karena syaratnya adalah  , maka diambil
, maka diambil  sebagai penyelesaiannya.
sebagai penyelesaiannya.
Dengan demikian, himpunan penyelesaian dari daerah yang berwarna adalah  .
.
Jadi, jawaban yang tepat adalah A.