Perhatikan gambar berikut ini! Dua tabung berbeda ukuran ditumpuk seperti pada gambar. Luas permukaan tumpukan dua tabung tersebut adalah ... cm2.

Pertanyaan

Perhatikan gambar berikut ini!

Dua tabung berbeda ukuran ditumpuk seperti pada gambar. Luas permukaan tumpukan dua tabung tersebut adalah $...\;\mathrm{cm}^2$ .

A. Sugianto

Master Teacher

Mahasiswa/Alumni Universitas Swadaya Gunung Jati Cirebon

Jawaban terverifikasi

Jawaban

luas permukaan tumpukan dua tabung adalah $2.640\;\mathrm{cm}^2$ .

Pembahasan

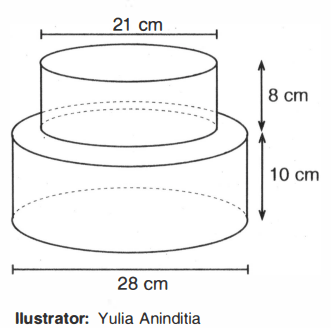
Jawaban yang tepat dari pertanyaan tersebut adalah $2.640\;\mathrm{cm}^2$ .

Ingat

Rumus luas permukaan tabung adalah sebagai berikut.

$\text{Luas permukaan tabung}=2\times\pi\times r\times(r+t)$

Rumus luas lingkaran adalah sebagai berikut.

$\text{Luas linghkaran}=\pi\times r^2$

Rumus hubungan antara jari-jari dengan diameter adalah sebagai berikut.

$\text{r}=\frac12\times\text{diameter}$

Soal tersebut berkaitan dengan luas permukaan gabungan pada bangun ruang sisi lengkung (tabung). Karena dua buah tabung bertumpuk, maka luas permukaan bangun gabungan tersebut adalah jumlah luas permukaan tabung yang besar dan luas permukaan tabung kecil dikurangi dengan dua kali luas daerah yang berhimpit.

Perhatikan tabung besar!
Jari-jari tabung besar didapat dengan cara :

$\begin{array}{rcl}r&=&\frac12\times28\\&=&14\end{array}$

Sehingga jari-jari tabung besar adalah $14\;\mathrm{cm}$ dan tingginya $10\;\mathrm{cm}$ .

Dengan menggunakan rumus luas permukaan tabung diperoleh:

$\begin{array}{rcl}\mathrm{Luas}\;\mathrm{permukaan}\;\mathrm{tabung}\;\mathrm{besa}r\;&=&\;2\times\pi\times r\times(r+t)\\&=&2\times\frac{22}7\times14\times(14+10)\\&=&2\times22\times2\times24\\&=&2.112\end{array}$

Sehingga luas permukaan tabung besar adalah $2.112\;\mathrm{cm}^2$ .

Perhatikan tabung kecil!
Jari-jari tabung kecil didapat dengan cara :

$\begin{array}{rcl}r&=&\frac12\times21\\&=&\frac{21}2\end{array}$

Sehingga jari-jari tabung besar adalah $\frac{21}2\;\mathrm{cm}$ dan tingginya $8\;\mathrm{cm}$ .

Dengan menggunakan rumus luas permukaan tabung diperoleh:
$\begin{array}{rcl}\mathrm{Luas}\;\mathrm{permukaan}\;\mathrm{tabung}\;\mathrm{kecil}\;&=&\;2\times\pi\times r\times(r+t)\\&=&2\times\frac{22}7\times\frac{21}2\times(\frac{21}2+8)\\&=&22\times3\times18,5\\&=&1.221\end{array}$

Sehingga luas permukaan tabung kecil adalah $1.221\;\mathrm{cm}^2$ .

Karena luas permukaan yang berimpit berbentuk lingkaran maka kita gunakan luas lingkaran untuk menentukan luas yang saling berimpit. Jari-jari yang digunakan adalah jari-jari pada tabung kecil (seperti pada gambar).

$\begin{array}{rcl}\mathrm{Luas}\;\mathrm{daerah}\;\mathrm{yang}\;\mathrm{berimpit}\;&=&\;\pi\times r^2\\&=&\frac{22}7\times\frac{21}2\times\frac{21}2\\&=&346,5\end{array}$

$\begin{array}{rcl}&&\mathrm{Luas}\;\mathrm{permukaan}\;\mathrm{tumpukan}\;\mathrm{dua}\;\mathrm{tabung}\;\\&=&\;\mathrm{luas}\;\mathrm{permukaan}\;\mathrm{tabung}\;\mathrm{besar}\;+\;\mathrm{luas}\;\mathrm{permukaan}\;\mathrm{tabung}\;\mathrm{kecil}\;-\;2\;\times\mathrm{luas}\;\mathrm{daerah}\;\mathrm{yang}\;\mathrm{berimpit}\\&=&2.112+1.221-2\times346,5\\&=&3.333-693\\&=&2.640\end{array}$

Dengan demikian luas permukaan tumpukan dua tabung adalah $2.640\;\mathrm{cm}^2$ .

720

3.7 (4 rating)

Muzhaffar Ibrahim