Pertanyaan

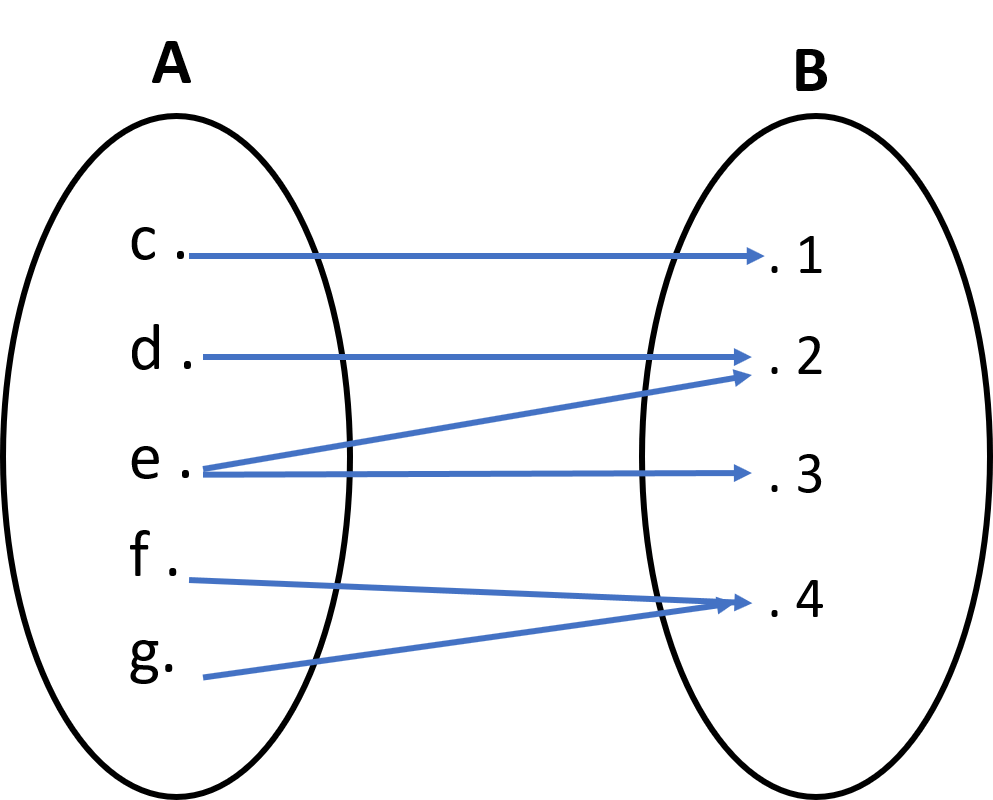
Diketahui himpunan pasangan berurutan { ( c , 1 ) , ( d , 2 ) , ( e , 2 ) , ( e , 3 ) , ( f , 4 ) , ( g , 4 ) } , sebutkan: a. Apakah himpunan pasangan termasuk pemetaan atau bukan b. Domain dan banyaknya anggota domain c. Kodomain dan banyaknya anggota kodomain d. Range dan banyaknya anggota range e. Buatlah diagram panah

Diketahui himpunan pasangan berurutan ${(c, 1), (d, 2), (e, 2), (e, 3), (f, 4), (g, 4)}$ , sebutkan:

a. Apakah himpunan pasangan termasuk pemetaan atau bukan

b. Domain dan banyaknya anggota domain

c. Kodomain dan banyaknya anggota kodomain

d. Range dan banyaknya anggota range

e. Buatlah diagram panah

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

M. Mariyam

Master Teacher

Mahasiswa/Alumni Institut Pertanian Bogor

Jawaban terverifikasi

Pembahasan

Ingat kembali konsep mengenai fungsi sebagai berikut: Fungsi (pemetaan) merupakan relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B. Semua anggota himpunan A atau daerah asal disebut domain , sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain . Hasil dari pemetaan antara domain dan kodomain disebut range fungsi atau daerah hasil. Sama halnya dengan relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, himpunan pasangan berurutan dan dengan diagram Cartesius. Oleh karena itu, diketahui himpunan pasangan berurutan maka kita dapat menjawab a. Himpunan pasangan berurutan bukan merupakan fungsi karena terdapat anggota himpunan A yang mempunyai pasangan lebih dari satu ke anggota himpunan B, yaitu . b. Domainterdiri dari anggota yaitu c. Kodomain terdiri dari anggota yaitu d. Rangeterdiri dari anggota yaitu e, Diagram panah sebagai berikut:

Ingat kembali konsep mengenai fungsi sebagai berikut:

Fungsi (pemetaan) merupakan relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B. Semua anggota himpunan A atau daerah asal disebut domain, sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain. Hasil dari pemetaan antara domain dan kodomain disebut range fungsi atau daerah hasil. Sama halnya dengan relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, himpunan pasangan berurutan dan dengan diagram Cartesius.

Oleh karena itu, diketahui himpunan pasangan berurutan open curly brackets open parentheses straight c comma 1 close parentheses comma open parentheses straight d comma 2 close parentheses comma open parentheses straight e comma 2 close parentheses comma open parentheses straight e comma 3 close parentheses comma open parentheses straight f comma 4 close parentheses comma open parentheses straight g comma 4 close parentheses close curly brackets maka kita dapat menjawab

a. Himpunan pasangan berurutan bukan merupakan fungsi karena terdapat anggota himpunan A yang mempunyai pasangan lebih dari satu ke anggota himpunan B, yaitu open parentheses e comma 2 close parentheses space dan space open parentheses e comma 3 close parentheses .

b. Domain terdiri dari anggota yaitu open curly brackets c comma space d comma space e comma space f comma space g close curly brackets

c. Kodomain terdiri dari anggota yaitu open curly brackets 1 comma space 2 comma space 3 comma space 4 close curly brackets

d. Range terdiri dari anggota yaitu open curly brackets 1 comma space 2 comma space 3 comma space 4 close curly brackets

e, Diagram panah sebagai berikut:

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

A = { 3 , 4 } , B = { 3 , 4 , 5 } dan relasi dari A ke B menyatakan "kurang dari". Nyatakan relasi tersebut dalam: b. himpunan pasangan berurutan

4.6

Jawaban terverifikasi

A = { 3 , 4 } , B = { 3 , 4 , 5 } dan relasi dari A ke B menyatakan "kurang dari". Nyatakan relasi tersebut dalam: a. diagram panah

4.4

Jawaban terverifikasi

A = { 3 , 4 } , B = { 3 , 4 , 5 } dan relasi dari A ke B menyatakan "kurang dari". Nyatakan relasi tersebut dalam: b. himpunan pasangan berurutan

4.6

Jawaban terverifikasi

A = { 3 , 4 } , B = { 3 , 4 , 5 } dan relasi dari A ke B menyatakan "kurang dari". Nyatakan relasi tersebut dalam: a. diagram panah

4.4

Jawaban terverifikasi

Diketahui P = { 2 , 3 , 4 , 5 , 6 } dan Q = { 6 , 7 , 8 , 9 , 10 , 11 , 12 } Tentukan relasi yang mungkin dari himpunan P ke himpunan Q. Sajikan relasi tersebut dalam bentuk diagram panah, pasangan b...

4.8

Jawaban terverifikasi