MM
Muhammad M
11 Juli 2022 14:55
Iklan
MM
Muhammad M
11 Juli 2022 14:55
Pertanyaan
Untuk masing-masing fungsi penerimaan total (TR) dan fungsi biaya total (TC) berikut ini, a. TR = 1088Q - 5Q2 dan TC = Q3-65Q2 +1520Q + 3.000 a. TR = 1120Q - Q2 dan TC = Q3-67Q2 +1600Q + 5.000 Gambarkan laba maksimum tersebut dalam grafik pendekatan total maupun pendekatan marginal
23
2
Iklan
AS
A. Selvi
Mahasiswa/Alumni Politeknik Negeri Ujung Pandang
13 Juli 2022 05:21
Jawaban terverifikasi
Jawabannya (gambar menyusul) Pembahasan: Diketahui: TR = 1.088Q - 5Q^2 TC = Q^3-65Q^2 +1.520Q + 3.000 Ditanyakan: grafik laba maksimum pendekatan total dan pendekatan marginal. Jawab: Laba maksimum dicapai saat MR = MC MR = TR' MR = 1.088Q - 5Q^2 MR = 1.088 - 10Q MC = TC' MC = Q^3-65Q^2 +1.520Q + 3.000 MC = 3Q^2 - 130Q + 1.520 MR = MC 1.088 - 10Q = 3Q^2 - 130Q + 1.520 3Q^2 - 130Q + 10Q + 1.520 - 1.088 = 0 3Q^2 - 120Q + 432 = 0 Mencari nilai Q menggunakan rumus persamaan kuadrat: a = 3, b = -120, dan c = 432 Q1,2 = (-b ± √(b^2 - 4ac))/2a Q1,2 = (-(-120) ± √((-120)^2 - 4(3)(432)))/2(3) Q1,2 = (120 ± √(14.400 - 5.184))/6 Q1,2 = (120 ± (120 - 72))/6 Q1,2 = (120 ± 48)/6 Q1 = (120 + 48)/6 = 28 (laba maksimum) atau Q2 = (120 - 48)/6 = 12 (rugi minimum) TR = 1.088Q - 5Q^2 TR = 1.088(28) - 5(28^2) TR = 30.464 - 3.920 TR = 26.544 TC = Q^3 - 65Q^2 +1.520Q + 3.000 TC = 28^3 - 65(28^2) + 1.520(28) + 3.000 TC = 21.952 - 50.960 + 42.560 + 3.000 TC = 16.552 Laba maksimum = TR - TC = 26.544 - 16.552 = 9.992 MR = 1.088 - 10Q MR = 1.088 - 10(28) MR = 808 (MR = P = AR) Gambar grafik dapat dilihat di bawah ini. (gambar menyusul) Note: jawaban hanya untuk poin A yang pertama, silahkan masukkan kembali ke forum untuk soal bagia A yang kedua.
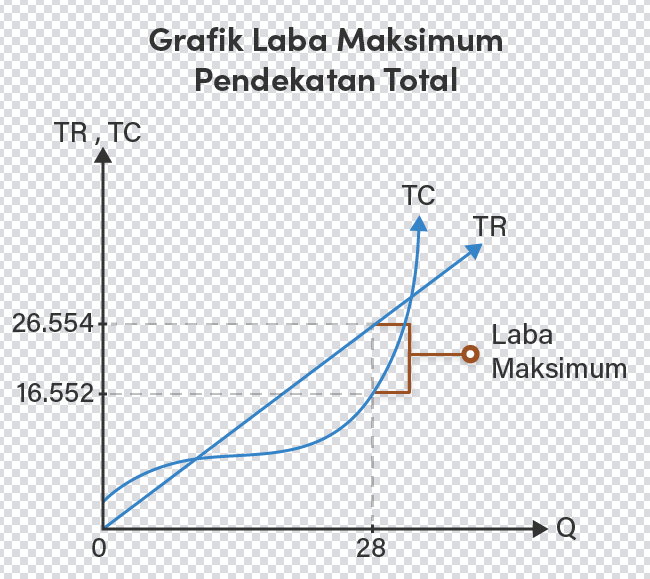
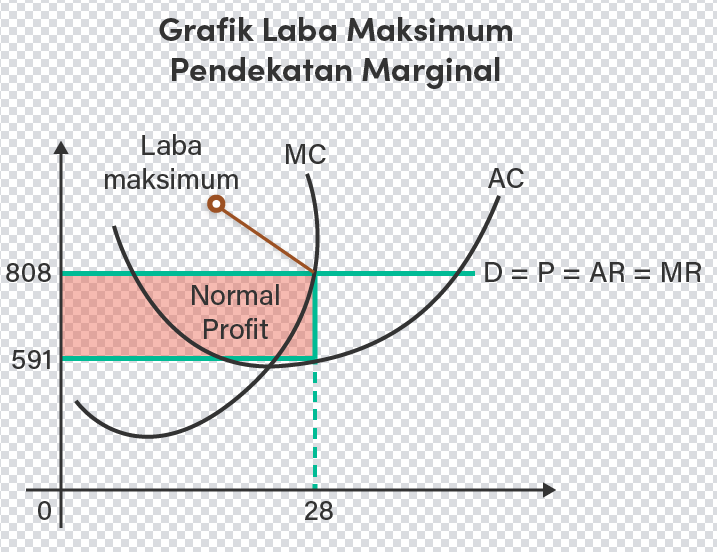
· 5.0 (2)
MK
Meysha K
17 Desember 2024 15:53
Dapat nilai 591 dari mana ya?
Iklan
NN
Nanda N
02 Desember 2024 12:04
Penerimaan total seorang produsen ditunjukkan oleh fungsi TR = 500Q – 3Q2 sedangkan biaya total yang dikeluarkan ditunjukkan oleh fungsi TC = 75Q2 + 3Q2. Berdasarkan data tersebut, tentukan jumlah output optimum dan jumlah keuntungan maksimum yang akan diperoleh produsen! Jika diketahui seorang produsen menghadapi kurva permintaan pasar P = 250 – 0,5Q sedangkan biaya rata-rata untuk menghasilkan produk adalah AC = 10Q + 50. Tentukan jumlah output optimum dan jumlah keuntungan maksimum yang akan diperoleh produsen!
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



