Zhafir Z
04 September 2024 23:39
Iklan
Zhafir Z
04 September 2024 23:39
Pertanyaan
undefined 1. int sin^4(5x) dx 2. int_(0)^(pi/2) sin^5 t dt 3. int_(0)^(pi/2) cos^6 t dt 4. int sin^7(3x) cos^3(3x) dx 5. int sin^4(2x) cos^4 x dx 6. int tan^6(2x) dx 7. int cot^4(2x) dx 8. int tan^(-3) x sec^2 x dx 9. int tan^5 x sec^(-3/2) x dx 10. int sec^4 x sqrt(tan x) dx 11. int cot^3 x csc^3 x dx 12. int cot^2(3x) csc(3x) dx 13. int sin(5x) cos(3x) dx
undefined 1. int sin^4(5x) dx 2. int_(0)^(pi/2) sin^5 t dt 3. int_(0)^(pi/2) cos^6 t dt 4. int sin^7(3x) cos^3(3x) dx 5. int sin^4(2x) cos^4 x dx 6. int tan^6(2x) dx 7. int cot^4(2x) dx 8. int tan^(-3) x sec^2 x dx 9. int tan^5 x sec^(-3/2) x dx 10. int sec^4 x sqrt(tan x) dx 11. int cot^3 x csc^3 x dx 12. int cot^2(3x) csc(3x) dx 13. int sin(5x) cos(3x) dx
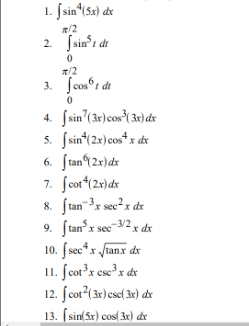
4
2
Iklan
Ace'S W
05 September 2024 13:41
<p>1 soal dulu, sedang menguatkan mental untuk pusing lagi 😭</p>
1 soal dulu, sedang menguatkan mental untuk pusing lagi 😭
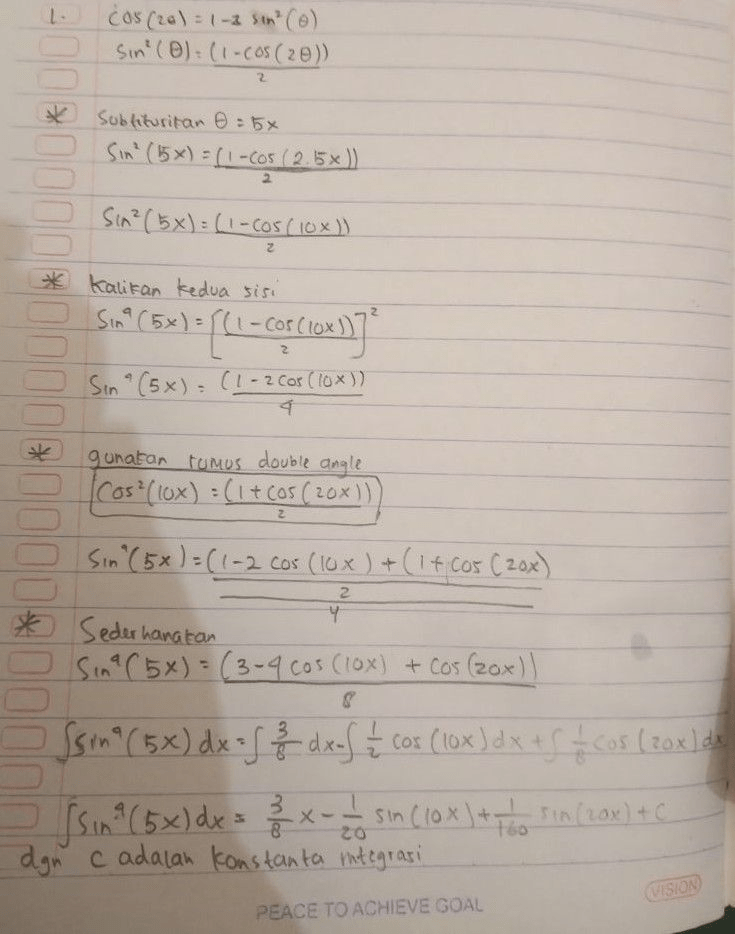
· 0.0 (0)
Iklan
ADAM M
07 September 2024 17:11
<p>Baik, mari kita selesaikan integral-integral trigonometri ini satu per satu.<br>1. ∫ sin⁴(5x) dx<br>Kita gunakan identitas trigonometri:<br>* sin² A = (1 - cos 2A) / 2<br>Maka,<br>* sin⁴(5x) = [sin²(5x)]²<br>* sin⁴(5x) = [(1 - cos 10x) / 2]²<br>* sin⁴(5x) = (1 - 2cos 10x + cos² 10x) / 4<br>Kita gunakan lagi identitas trigonometri untuk cos² 10x:<br>* cos² A = (1 + cos 2A) / 2<br>Maka,<br>* cos² 10x = (1 + cos 20x) / 2<br>Substitusikan ke persamaan sin⁴(5x):<br>* sin⁴(5x) = (1 - 2cos 10x + [(1 + cos 20x) / 2]) / 4<br>* sin⁴(5x) = (1/4) - (1/2)cos 10x + (1/8) + (1/8)cos 20x<br>* sin⁴(5x) = (3/8) - (1/2)cos 10x + (1/8)cos 20x<br>Sekarang kita integralkan:<br>∫ sin⁴(5x) dx<br>= ∫ [(3/8) - (1/2)cos 10x + (1/8)cos 20x] dx<br>= (3/8)x - (1/20)sin 10x + (1/160)sin 20x + C<br>Jawaban 1: (3/8)x - (1/20)sin 10x + (1/160)sin 20x + C</p><p><br>2. ∫₀^(π/2) sin⁵ t dt<br>Kita gunakan teknik reduksi pangkat:<br>* ∫ sin^n x dx = - (1/n) sin^(n-1) x cos x + ((n-1)/n) ∫ sin^(n-2) x dx<br>Maka, untuk n = 5:<br>∫ sin⁵ t dt<br>= - (1/5) sin⁴ t cos t + (4/5) ∫ sin³ t dt<br>Untuk n = 3:<br>∫ sin³ t dt<br>= - (1/3) sin² t cos t + (2/3) ∫ sin t dt<br>= - (1/3) sin² t cos t - (2/3) cos t<br>Substitusikan kembali:<br>∫ sin⁵ t dt<br>= - (1/5) sin⁴ t cos t + (4/5) [ - (1/3) sin² t cos t - (2/3) cos t]<br>= - (1/5) sin⁴ t cos t - (4/15) sin² t cos t - (8/15) cos t<br>Sekarang kita hitung integral tentu:<br>∫₀^(π/2) sin⁵ t dt<br>= [- (1/5) sin⁴ t cos t - (4/15) sin² t cos t - (8/15) cos t] dari 0 sampai π/2<br>= [0 - 0 - 0] - [- 0 - 0 - (8/15)]<br>= 8/15<br>Jawaban 2: 8/15</p><p><br>3. ∫₀^(π/2) cos⁶ t dt<br>Mirip dengan soal nomor 2, kita gunakan teknik reduksi pangkat:<br>* ∫ cos^n x dx = (1/n) cos^(n-1) x sin x + ((n-1)/n) ∫ cos^(n-2) x dx<br>Maka, untuk n = 6:<br>∫ cos⁶ t dt<br>= (1/6) cos⁵ t sin t + (5/6) ∫ cos⁴ t dt<br>Untuk n = 4<br>∫ cos⁴ t dt<br>= (1/4) cos³ t sin t + (3/4) ∫ cos² t dt<br>Untuk n = 2<br>∫ cos² t dt<br>= (1/2) cos t sin t + (1/2) ∫ 1 dt<br>= (1/2) cos t sin t + (1/2) t<br>Substitusikan kembali:<br>∫ cos⁴ t dt<br>= (1/4) cos³ t sin t + (3/4) [(1/2) cos t sin t + (1/2) t]<br>= (1/4) cos³ t sin t + (3/8) cos t sin t + (3/8) t<br>∫ cos⁶ t dt<br>= (1/6) cos⁵ t sin t + (5/6) [(1/4) cos³ t sin t + (3/8) cos t sin t + (3/8) t]<br>= (1/6) cos⁵ t sin t + (5/24) cos³ t sin t + (15/48) cos t sin t + (15/48) t<br>Sekarang kita hitung integral tentu:<br>∫₀^(π/2) cos⁶ t dt<br>= [(1/6) cos⁵ t sin t + (5/24) cos³ t sin t + (15/48) cos t sin t + (15/48) t] dari 0 sampai π/2<br>= [0 + 0 + 0 + (15/48)(π/2)] - [0 + 0 + 0 + 0]<br>= (15/96)π<br>Jawaban 3: (15/96)π</p>
Baik, mari kita selesaikan integral-integral trigonometri ini satu per satu.
1. ∫ sin⁴(5x) dx
Kita gunakan identitas trigonometri:
* sin² A = (1 - cos 2A) / 2
Maka,
* sin⁴(5x) = [sin²(5x)]²
* sin⁴(5x) = [(1 - cos 10x) / 2]²
* sin⁴(5x) = (1 - 2cos 10x + cos² 10x) / 4
Kita gunakan lagi identitas trigonometri untuk cos² 10x:
* cos² A = (1 + cos 2A) / 2
Maka,
* cos² 10x = (1 + cos 20x) / 2
Substitusikan ke persamaan sin⁴(5x):
* sin⁴(5x) = (1 - 2cos 10x + [(1 + cos 20x) / 2]) / 4
* sin⁴(5x) = (1/4) - (1/2)cos 10x + (1/8) + (1/8)cos 20x
* sin⁴(5x) = (3/8) - (1/2)cos 10x + (1/8)cos 20x
Sekarang kita integralkan:
∫ sin⁴(5x) dx
= ∫ [(3/8) - (1/2)cos 10x + (1/8)cos 20x] dx
= (3/8)x - (1/20)sin 10x + (1/160)sin 20x + C
Jawaban 1: (3/8)x - (1/20)sin 10x + (1/160)sin 20x + C
2. ∫₀^(π/2) sin⁵ t dt
Kita gunakan teknik reduksi pangkat:
* ∫ sin^n x dx = - (1/n) sin^(n-1) x cos x + ((n-1)/n) ∫ sin^(n-2) x dx
Maka, untuk n = 5:
∫ sin⁵ t dt
= - (1/5) sin⁴ t cos t + (4/5) ∫ sin³ t dt
Untuk n = 3:
∫ sin³ t dt
= - (1/3) sin² t cos t + (2/3) ∫ sin t dt
= - (1/3) sin² t cos t - (2/3) cos t
Substitusikan kembali:
∫ sin⁵ t dt
= - (1/5) sin⁴ t cos t + (4/5) [ - (1/3) sin² t cos t - (2/3) cos t]
= - (1/5) sin⁴ t cos t - (4/15) sin² t cos t - (8/15) cos t
Sekarang kita hitung integral tentu:
∫₀^(π/2) sin⁵ t dt
= [- (1/5) sin⁴ t cos t - (4/15) sin² t cos t - (8/15) cos t] dari 0 sampai π/2
= [0 - 0 - 0] - [- 0 - 0 - (8/15)]
= 8/15
Jawaban 2: 8/15
3. ∫₀^(π/2) cos⁶ t dt
Mirip dengan soal nomor 2, kita gunakan teknik reduksi pangkat:
* ∫ cos^n x dx = (1/n) cos^(n-1) x sin x + ((n-1)/n) ∫ cos^(n-2) x dx
Maka, untuk n = 6:
∫ cos⁶ t dt
= (1/6) cos⁵ t sin t + (5/6) ∫ cos⁴ t dt
Untuk n = 4
∫ cos⁴ t dt
= (1/4) cos³ t sin t + (3/4) ∫ cos² t dt
Untuk n = 2
∫ cos² t dt
= (1/2) cos t sin t + (1/2) ∫ 1 dt
= (1/2) cos t sin t + (1/2) t
Substitusikan kembali:
∫ cos⁴ t dt
= (1/4) cos³ t sin t + (3/4) [(1/2) cos t sin t + (1/2) t]
= (1/4) cos³ t sin t + (3/8) cos t sin t + (3/8) t
∫ cos⁶ t dt
= (1/6) cos⁵ t sin t + (5/6) [(1/4) cos³ t sin t + (3/8) cos t sin t + (3/8) t]
= (1/6) cos⁵ t sin t + (5/24) cos³ t sin t + (15/48) cos t sin t + (15/48) t
Sekarang kita hitung integral tentu:
∫₀^(π/2) cos⁶ t dt
= [(1/6) cos⁵ t sin t + (5/24) cos³ t sin t + (15/48) cos t sin t + (15/48) t] dari 0 sampai π/2
= [0 + 0 + 0 + (15/48)(π/2)] - [0 + 0 + 0 + 0]
= (15/96)π
Jawaban 3: (15/96)π
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



