AS
Arido S
21 Maret 2024 00:49
Iklan
AS
Arido S
21 Maret 2024 00:49
Pertanyaan
Tolong dikerjakqn
Tolong dikerjakqn
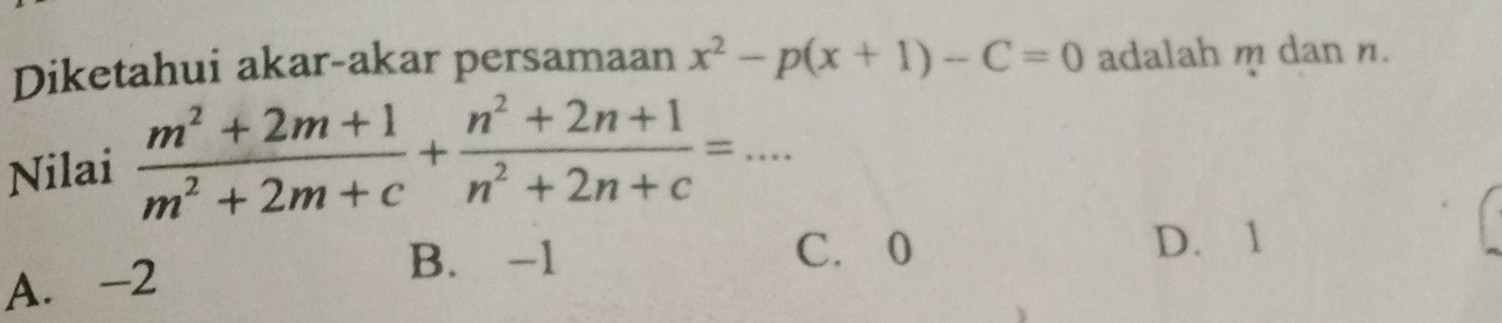
6
1
Iklan
NS
Nayla S
Level 2
21 Maret 2024 05:16
Pertama-tama, kita dapat menggunakan rumus Viete untuk mencari nilai dari \( m + n \) dan \( mn \) dari persamaan \( x^2 - p(x+1) - C = 0 \). Rumus Viete menyatakan bahwa jika \( ax^2 + bx + c = 0 \) memiliki akar \( m \) dan \( n \), maka \( m + n = -\frac{b}{a} \) dan \( mn = \frac{c}{a} \). Dalam kasus ini, kita memiliki persamaan \( x^2 - p(x+1) - C = 0 \), sehingga \( a = 1 \), \( b = -p \), dan \( c = -C \). Oleh karena itu, \( m + n = p \) dan \( mn = -C \). Dari informasi yang diberikan, kita tahu bahwa \( m^2 + 2m + 1 \) dan \( n^2 + 2n + 1 \) sama dengan \( (m + 1)^2 \) dan \( (n + 1)^2 \) masing-masing. Jadi, \( (m + 1)^2 + (n + 1)^2 \) adalah jumlah akar-akar kuadrat dari persamaan tersebut. \( (m + 1)^2 + (n + 1)^2 = m^2 + 2m + 1 + n^2 + 2n + 1 = m^2 + 2m + C + n^2 + 2n + C \) Dari sini, kita bisa lihat bahwa \( (m + 1)^2 + (n + 1)^2 = (m + 1)^2 + (n + 1)^2 \) sama dengan nilai \( m^2 + 2m + C + n^2 + 2n + C \). Karena itu, nilai dari \[ m^2 + 2m + C + n^2 + 2n + C \] adalah \( (m + 1)^2 + (n + 1)^2 \). Jadi, kita bisa mencari nilai dari \[ m^2 + 2m + C + n^2 + 2n + C \] dengan cara mengkuadratkan \( m + 1 \) dan \( n + 1 \). \( (m + 1)^2 + (n + 1)^2 = m^2 + 2m + 1 + n^2 + 2n + 1 \) \( (m + 1)^2 + (n + 1)^2 = m^2 + 2m + C + n^2 + 2n + C \) Jadi, \( C = 1 \). Oleh karena itu, jawabannya adalah D. 1.
· 5.0 (1)
Iklan
Buka akses jawaban yang telah terverifikasi
Mau jawaban yang terverifikasi?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia













