Rafaiza A
12 Maret 2025 05:53
Iklan
Rafaiza A
12 Maret 2025 05:53
Pertanyaan
tolong dibantu π
tolong dibantu π
1
3
Iklan
E. Nur
12 Maret 2025 15:53
Pembahasan pada gambar terlampir
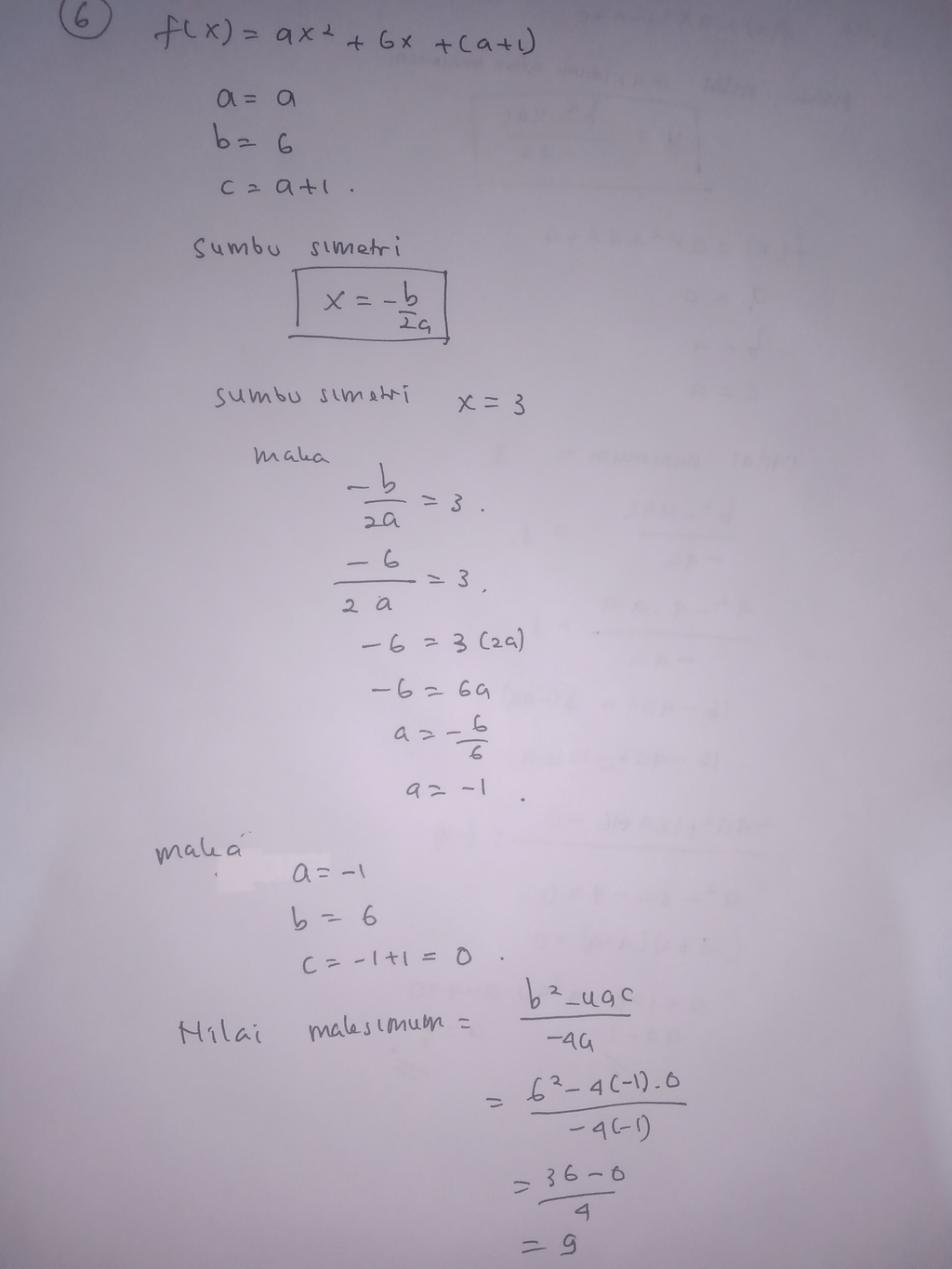
Β· 5.0 (1)
Iklan
Mario A
12 Maret 2025 07:46
<p>Jika xs menyatakan sumbu simetri untuk f(x) = ax^2+bx+c maka xs = -b/2a. Dari soal, karena f(x) = ax^2+6x+(a+1) memiliki sumbu simetri di xs = 3, maka -6/2a = 3 -> a = -6/(2.3) = -1. Akibatnya, f(x) = -x^2+6x. Nilai maksimum fungsi adalah pemetaan sumbu simetri ke y oleh f. Dengan kata lain, nilai maksimum fungsi adalah f(xs) = f(3) = -(3^2)+6(3) = -9+18 = 9</p>
Jika xs menyatakan sumbu simetri untuk f(x) = ax^2+bx+c maka xs = -b/2a. Dari soal, karena f(x) = ax^2+6x+(a+1) memiliki sumbu simetri di xs = 3, maka -6/2a = 3 -> a = -6/(2.3) = -1. Akibatnya, f(x) = -x^2+6x. Nilai maksimum fungsi adalah pemetaan sumbu simetri ke y oleh f. Dengan kata lain, nilai maksimum fungsi adalah f(xs) = f(3) = -(3^2)+6(3) = -9+18 = 9
Β· 0.0 (0)
Rafaiza A
12 Maret 2025 13:08
maaf kak sayaa masihh bingung π
Dafa R
16 Maret 2025 03:45
<p>Sumbu simetri dari fungsi kuadrat f(x)=ax2+6x+(a+1)f(x) = ax^2 + 6x + (a+1) diberikan oleh rumus:</p><p>x=βb2ax = \frac{-b}{2a}</p><p>Diketahui bahwa sumbu simetri adalah x=3x = 3, sehingga:</p><p>3=β62a3 = \frac{-6}{2a} 3Γ2a=β63 \times 2a = -6 6a=β66a = -6 a=β1a = -1</p><p>Sekarang, substitusi a=β1a = -1 ke dalam fungsi:</p><p>f(x)=(β1)x2+6x+(β1+1)f(x) = (-1)x^2 + 6x + (-1 + 1) f(x)=βx2+6xf(x) = -x^2 + 6x</p><p>Maksimum dari fungsi kuadrat terjadi pada titik sumbu simetri, yaitu x=3x = 3. Substitusi x=3x = 3 ke dalam f(x)f(x):</p><p>f(3)=β(3)2+6(3)f(3) = -(3)^2 + 6(3) =β9+18= -9 + 18 =9= 9</p><p>Jadi, nilai maksimum fungsi tersebut adalah <strong>9</strong>.</p>
Sumbu simetri dari fungsi kuadrat f(x)=ax2+6x+(a+1)f(x) = ax^2 + 6x + (a+1) diberikan oleh rumus:
x=βb2ax = \frac{-b}{2a}
Diketahui bahwa sumbu simetri adalah x=3x = 3, sehingga:
3=β62a3 = \frac{-6}{2a} 3Γ2a=β63 \times 2a = -6 6a=β66a = -6 a=β1a = -1
Sekarang, substitusi a=β1a = -1 ke dalam fungsi:
f(x)=(β1)x2+6x+(β1+1)f(x) = (-1)x^2 + 6x + (-1 + 1) f(x)=βx2+6xf(x) = -x^2 + 6x
Maksimum dari fungsi kuadrat terjadi pada titik sumbu simetri, yaitu x=3x = 3. Substitusi x=3x = 3 ke dalam f(x)f(x):
f(3)=β(3)2+6(3)f(3) = -(3)^2 + 6(3) =β9+18= -9 + 18 =9= 9
Jadi, nilai maksimum fungsi tersebut adalah 9.
Β· 5.0 (1)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!
LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian
Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
