Giffari H
26 Agustus 2023 15:38
Iklan
Giffari H
26 Agustus 2023 15:38
Pertanyaan
Tolong bantuan nya Kalau bisa pake kertas jawabnya biar tambah ngerti Makasih
Tolong bantuan nya
Kalau bisa pake kertas jawabnya biar tambah ngerti
Makasih

3
2
Iklan
Sadrina A
26 Agustus 2023 15:53
<p>Yang perlu kita ingat adalah rumus-rumus dari trigonometri.</p><p>sin x + sin y = 2sin(x+y/2)cos(x-y/2)</p><p>sin x - sin y = 2cos(x+y/2)sin(x-y/2)</p><p>cos x + cos y = 2cos(x+y/2)cos(x-y/2)</p><p>cos x - cos y = -2sin(x+y/2)sin(x-y/2)</p>
Yang perlu kita ingat adalah rumus-rumus dari trigonometri.
sin x + sin y = 2sin(x+y/2)cos(x-y/2)
sin x - sin y = 2cos(x+y/2)sin(x-y/2)
cos x + cos y = 2cos(x+y/2)cos(x-y/2)
cos x - cos y = -2sin(x+y/2)sin(x-y/2)
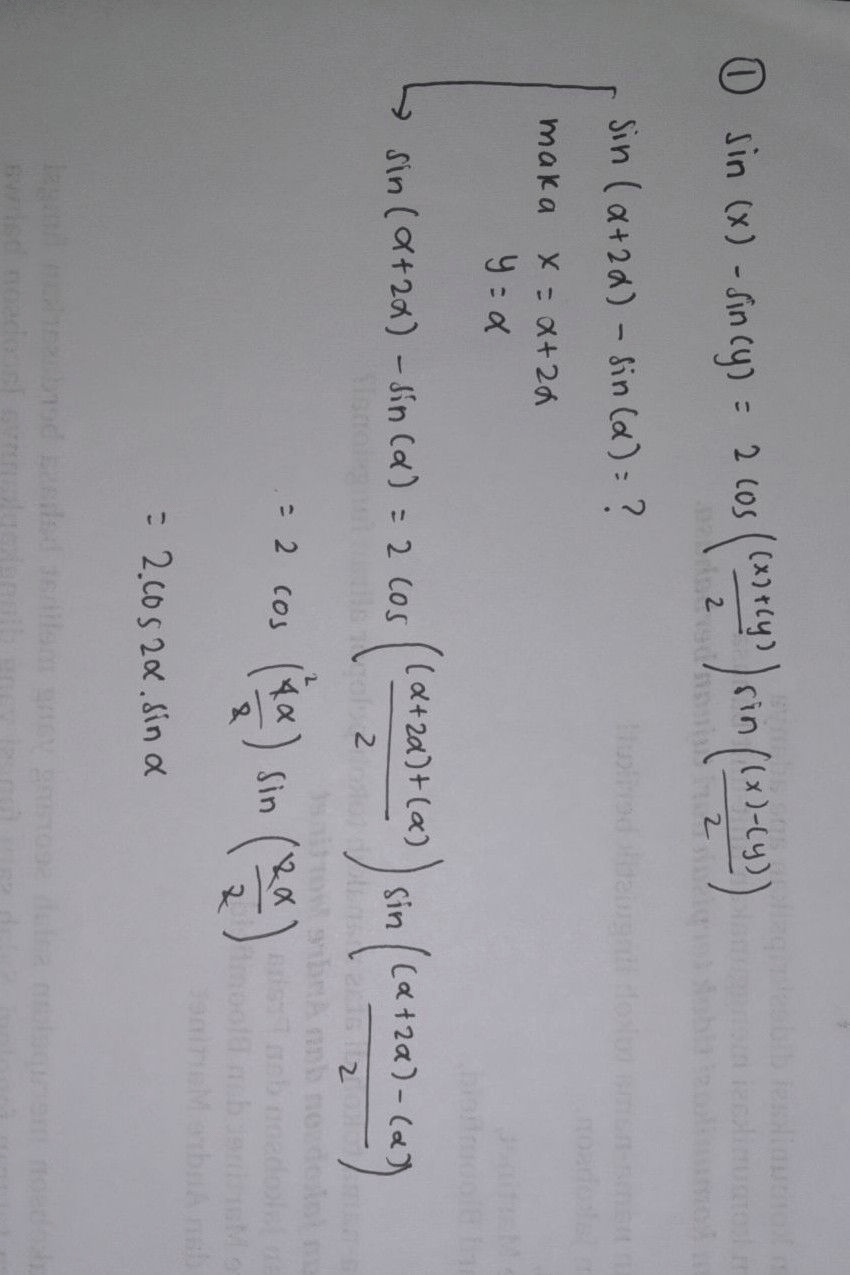
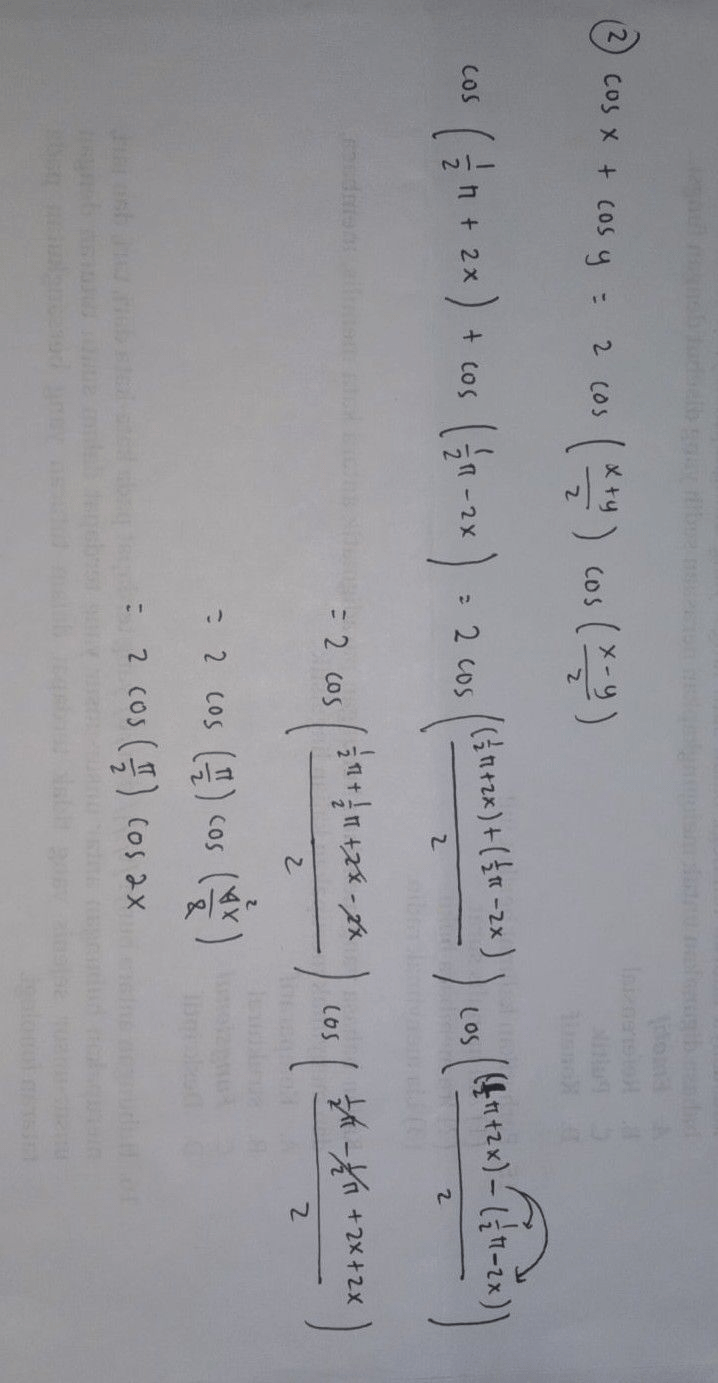
· 0.0 (0)
Iklan
Agung D
26 Agustus 2023 19:08
<h1><i><strong><u>Untuk soal 5a</u></strong></i><br><br>Bentuk dari sin (a + 2a) - sin a dalam bentuk perkalian yang paling sederhana adalah 2 sin a cos a.</h1><p>Pada trigonometri, ada yang namanya rumus double angle, yang menyatakan bahwa sin 2a = 2 sin a cos a. Dengan menggunakan rumus ini, kita bisa langsung mendapatkan bentuk perkalian dari sin (a + 2a) - sin a, yaitu 2 sin a cos a.</p><p>Berikut adalah skema pembuktiannya:</p><p>sin (a + 2a) - sin a = sin a + sin 2a - sin a = sin a + 2 sin a cos a - sin a = 2 sin a cos a<br><br>penjelasan tembahan:<br>Rumus sin 2a = 2 sin a cos a dapat dibuktikan dengan menggunakan rumus jumlah dan selisih trigonometri.</p><p>Pada rumus <i><strong>jumlah</strong></i> trigonometri, <u>sin (a + b) = sin a cos b + cos a sin b</u>.</p><p>Pada rumus <i><strong>selisih</strong></i> trigonometri, <u>sin (a - b) = sin a cos b - cos a sin b</u>.</p><p><strong>Jika kita substitusi a = a dan b = a</strong>, maka diperoleh:</p><p>sin (2a) = sin a cos a + cos a sin a</p><p>sin (2a) = 2 sin a cos a</p><p>Jadi, sin 2a = 2 sin a cos a.</p><p>Berikut adalah skema pembuktiannya:</p><p>sin (2a) = sin (a + a) = sin a cos a + cos a sin a = 2 sin a cos a</p><p>Rumus ini dapat digunakan untuk menyederhanakan ekspresi trigonometri yang melibatkan sudut rangkap.</p><p><br>Semoga ini membantu.</p><p> </p><h1><i><strong><u>Untuk soal 5b</u></strong></i></h1><p> </p><p>Ekspresi pada gambar dapat diekspresikan dalam bentuk perkalian sebagai berikut:</p><h2><strong>cos (π/2 + 2x) + cos (π/2 - 2x) = 2cos(2x)</strong></h2><p>Ekspresi pertama dapat disederhanakan dengan menggunakan identitas trigonometri berikut:</p><p>cos(a + b) + cos(a - b) = 2cos(a)cos(b)</p><p>Pada kasus ini, a = π/2 dan b = 2x. Substitusi nilai-nilai ini ke dalam identitas, kita dapatkan:</p><p>cos(π/2 + 2x) + cos(π/2 - 2x) = 2cos(π/2)cos(2x) = 2 * 1 * cos(2x) = 2cos(2x)</p><p>Ekspresi kedua dapat disederhanakan menggunakan identitas yang sama. Dalam hal ini, a = π/2 dan b = -2x. Substitusi nilai-nilai ini ke dalam identitas, kita dapatkan:</p><p>cos(π/2 - 2x) + cos(π/2 + 2x) = 2cos(π/2)cos(-2x) = 2 * 1 * cos(-2x) = 2cos(2x)</p><p>Oleh karena itu, kedua ekspresi dapat diekspresikan dalam bentuk perkalian sebagai 2cos(2x).</p>
Untuk soal 5a
Bentuk dari sin (a + 2a) - sin a dalam bentuk perkalian yang paling sederhana adalah 2 sin a cos a.
Pada trigonometri, ada yang namanya rumus double angle, yang menyatakan bahwa sin 2a = 2 sin a cos a. Dengan menggunakan rumus ini, kita bisa langsung mendapatkan bentuk perkalian dari sin (a + 2a) - sin a, yaitu 2 sin a cos a.
Berikut adalah skema pembuktiannya:
sin (a + 2a) - sin a = sin a + sin 2a - sin a = sin a + 2 sin a cos a - sin a = 2 sin a cos a
penjelasan tembahan:
Rumus sin 2a = 2 sin a cos a dapat dibuktikan dengan menggunakan rumus jumlah dan selisih trigonometri.
Pada rumus jumlah trigonometri, sin (a + b) = sin a cos b + cos a sin b.
Pada rumus selisih trigonometri, sin (a - b) = sin a cos b - cos a sin b.
Jika kita substitusi a = a dan b = a, maka diperoleh:
sin (2a) = sin a cos a + cos a sin a
sin (2a) = 2 sin a cos a
Jadi, sin 2a = 2 sin a cos a.
Berikut adalah skema pembuktiannya:
sin (2a) = sin (a + a) = sin a cos a + cos a sin a = 2 sin a cos a
Rumus ini dapat digunakan untuk menyederhanakan ekspresi trigonometri yang melibatkan sudut rangkap.
Semoga ini membantu.
Untuk soal 5b
Ekspresi pada gambar dapat diekspresikan dalam bentuk perkalian sebagai berikut:
cos (π/2 + 2x) + cos (π/2 - 2x) = 2cos(2x)
Ekspresi pertama dapat disederhanakan dengan menggunakan identitas trigonometri berikut:
cos(a + b) + cos(a - b) = 2cos(a)cos(b)
Pada kasus ini, a = π/2 dan b = 2x. Substitusi nilai-nilai ini ke dalam identitas, kita dapatkan:
cos(π/2 + 2x) + cos(π/2 - 2x) = 2cos(π/2)cos(2x) = 2 * 1 * cos(2x) = 2cos(2x)
Ekspresi kedua dapat disederhanakan menggunakan identitas yang sama. Dalam hal ini, a = π/2 dan b = -2x. Substitusi nilai-nilai ini ke dalam identitas, kita dapatkan:
cos(π/2 - 2x) + cos(π/2 + 2x) = 2cos(π/2)cos(-2x) = 2 * 1 * cos(-2x) = 2cos(2x)
Oleh karena itu, kedua ekspresi dapat diekspresikan dalam bentuk perkalian sebagai 2cos(2x).
· 0.0 (0)
Mau jawaban yang terverifikasi?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



