Rafaiza A

12 Maret 2025 05:50
Iklan
Rafaiza A

12 Maret 2025 05:50
Pertanyaan
tolong bantu saya di soal yg E saja 🙏
tolong bantu saya di soal yg E saja 🙏

1
2
Iklan
E. Nur
12 Maret 2025 15:46
Pembahasan pada gambar terlampir
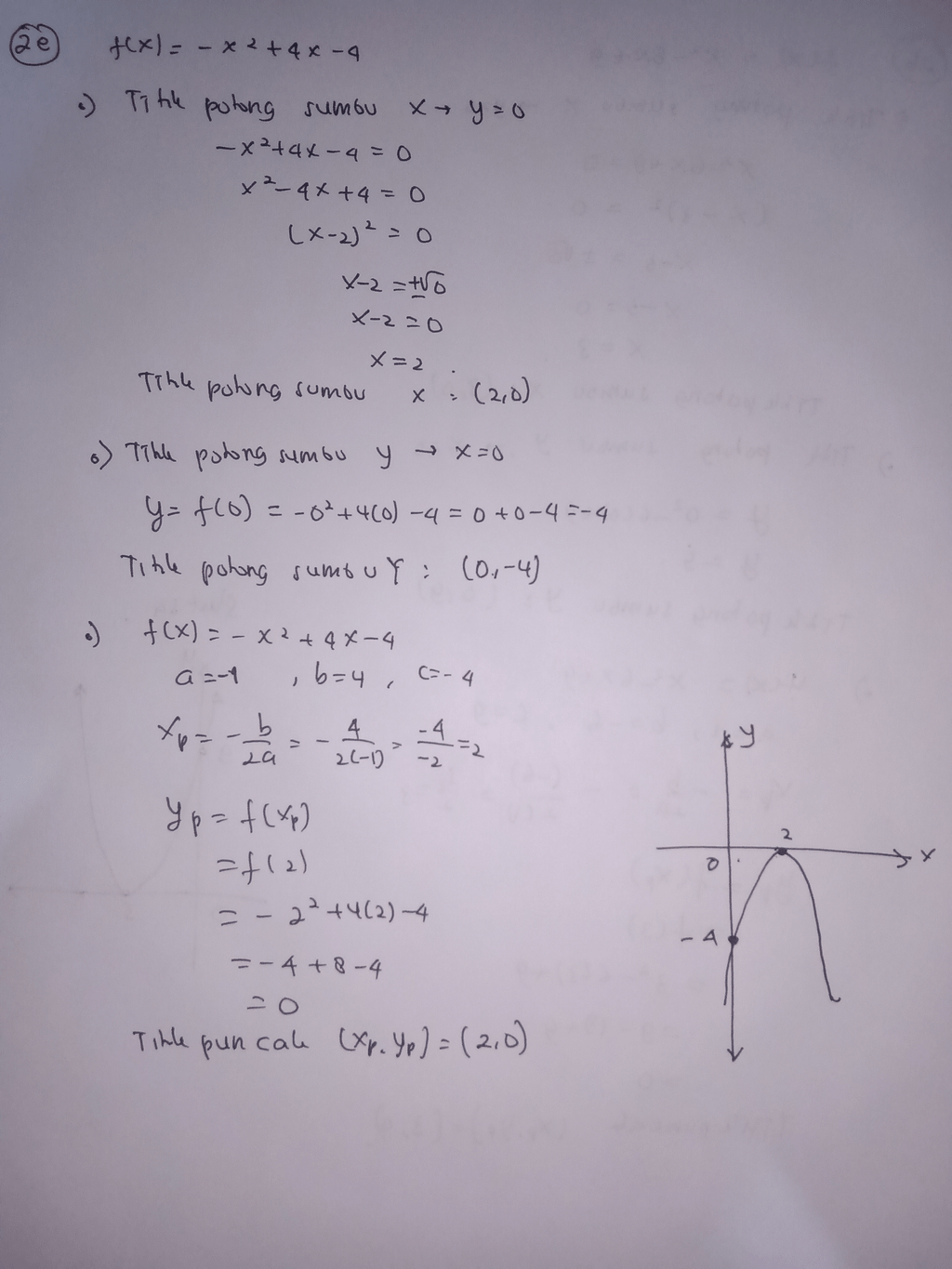
· 5.0 (2)
Wandykranggmail.Com W
13 Maret 2025 14:03
8 75 _4 6 24
Iklan
Suci S
12 Maret 2025 12:49
<p>f(x) = -x<sup>2 </sup>+4x - 4</p><p><strong>Sumbu simetri</strong></p><p>x = -b / 2a</p><p>Dengan a = -1 dan b = 4, maka:</p><p>x = -4 / 2(-1)</p><p>x = 2</p><p>Jadi, sumbu simetri adalah x = 2</p><p><strong>Titik Puncak</strong></p><p>titik puncak adalah (x, f(x)) dengan x = 2</p><p>f (-3) = -(2)<sup>2</sup> + 4 (2) - 4 = 0</p><p>Jadi, titik puncak adalah (2,0)</p><p><strong>Titik potong Sumbu y</strong></p><p>f (0) = -(0)<sup>2</sup> + 4 (0) - 4 = -4</p><p>Jadi, titik potong dengan sumbu y adalah (0,-4)</p><p><strong>Titik Potong sumbu x</strong></p><p>-x<sup>2 </sup>+4x - 4 (dikali -1)</p><p>x<sup>2 </sup> - 4x + 4 (difaktorkan)</p><p>(x - 2) (x - 2)</p><p>x = 2</p><p>Jadi, titik potong dengan sumbu x adalah (2,0)</p><p><strong>Jenisnya</strong></p><p>Karena a = -1 (negatif), maka grafiknya berbentuk <strong>parabola terbuka ke bawah</strong>, sehingga titik puncak merupakan <strong>titik maksimum</strong>.</p>
f(x) = -x2 +4x - 4
Sumbu simetri
x = -b / 2a
Dengan a = -1 dan b = 4, maka:
x = -4 / 2(-1)
x = 2
Jadi, sumbu simetri adalah x = 2
Titik Puncak
titik puncak adalah (x, f(x)) dengan x = 2
f (-3) = -(2)2 + 4 (2) - 4 = 0
Jadi, titik puncak adalah (2,0)
Titik potong Sumbu y
f (0) = -(0)2 + 4 (0) - 4 = -4
Jadi, titik potong dengan sumbu y adalah (0,-4)
Titik Potong sumbu x
-x2 +4x - 4 (dikali -1)
x2 - 4x + 4 (difaktorkan)
(x - 2) (x - 2)
x = 2
Jadi, titik potong dengan sumbu x adalah (2,0)
Jenisnya
Karena a = -1 (negatif), maka grafiknya berbentuk parabola terbuka ke bawah, sehingga titik puncak merupakan titik maksimum.
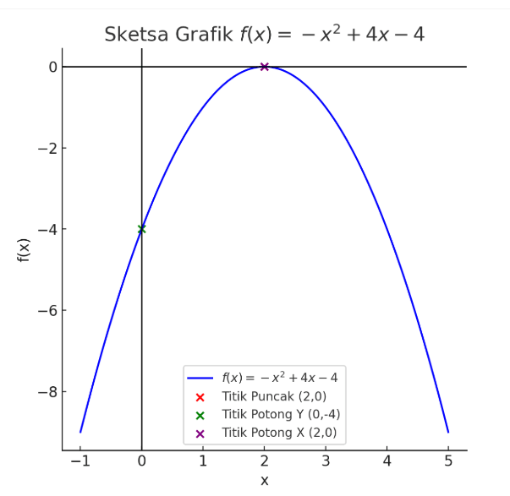
· 5.0 (1)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



