Salwa P
27 Februari 2023 07:25
Iklan
Salwa P
27 Februari 2023 07:25
Pertanyaan
Tentukan penyelesaian dari setiap pertidaksamaan logaritma berikut. log (3 + x) + log 4 ≥ 2 log x
1
1
Iklan
P. Vidya
Mahasiswa/Alumni Universitas Negeri Malang
28 Februari 2023 23:48
<p>Halo Salwa. Kakak bantu jawab ya.</p><p>Jawab: -2≤x≤6</p><p>Pembahasan:</p><p>Ingat!</p><ul><li>Untuk a>1.</li></ul><p><sup>a</sup>log f(x) ≥ <sup>a</sup>log g(x) maka f(x) ≥ g(x). Syarat numerus f(x),g(x)>0.</p><ul><li><sup>a</sup>log b + <sup>a</sup>log c = <sup>a</sup>log (b×c).</li><li><sup>a</sup>log b<sup>n</sup> = n <sup>a</sup>log b</li></ul><p>Dengan menggunakan konsep di atas, diperoleh</p><p>Langkah 1. Menentukan solusi umum.</p><p>log(3+x) + log 4 ≥ 2 log x</p><p> log ((3+x)(4)) ≥ log x<sup>2</sup></p><p> log (12+4x) ≥ log x<sup>2</sup></p><p>Sehingga (12+4x) ≥ x<sup>2</sup></p><p>Diperoleh,</p><p> (12+4x) ≥ x<sup>2</sup></p><p>-x<sup>2</sup>+4x+12 ≥ 0</p><p> x<sup>2</sup>-4x-12 ≤ 0 (kedua ruas dikali -1 sehingga tandanya jadi ≤)</p><p>Pembuat nolnya adalah</p><p> x<sup>2</sup>-4x-12 = 0</p><p>(x-6)(x+2) = 0</p><p> x-6 = 0 atau x+2 = 0</p><p> x = 6 x = -2</p><p>Perhatikan gambar (i) berikut!</p><p>Uji titik untuk menentukan tanda pada setiap interval.</p><p>x = -5 maka diperoleh hasil berupa bilangan positif.</p><p>x = 0 maka diperoleh hasil berupa bilangan negatif.</p><p>x = 10 maka diperoleh hasil berupa bilangan positif.</p><p>Noktahnya bulat penuh karena tanda pertidaksamaannya ≤.</p><p>Karena tandanya ≤, pilih daerah yang negatif. </p><p>Sehingga, penyelesaiannya adalah -2≤x≤6.</p><p>Langkah 2. Menentukan syarat umerus.</p><p>(12+4x) > 0 dan x<sup>2</sup> > 0.</p><p>(12+4x) > 0</p><p> 4x > -12</p><p> x > -3</p><p>Dan, </p><p>x<sup>2</sup> > 0, maka x∈R.</p><p>Sehingga, untuk syarat numerus diperoleh batas x> -3.</p><p>Langkah 3. Menentukan penyelesaian.</p><p>Penyelesaiannya adalah irisan dari -2≤x≤6 dan x> -3.</p><p>Perhatikan gambar (ii) berikut!</p><p>Sehingga, penyelesaiannya adalah -2≤x≤6.</p><p> </p><p><strong><u>Jadi, jawaban yang benar adalah -2≤x≤6.</u></strong></p>
Halo Salwa. Kakak bantu jawab ya.
Jawab: -2≤x≤6
Pembahasan:
Ingat!
- Untuk a>1.
alog f(x) ≥ alog g(x) maka f(x) ≥ g(x). Syarat numerus f(x),g(x)>0.
- alog b + alog c = alog (b×c).
- alog bn = n alog b
Dengan menggunakan konsep di atas, diperoleh
Langkah 1. Menentukan solusi umum.
log(3+x) + log 4 ≥ 2 log x
log ((3+x)(4)) ≥ log x2
log (12+4x) ≥ log x2
Sehingga (12+4x) ≥ x2
Diperoleh,
(12+4x) ≥ x2
-x2+4x+12 ≥ 0
x2-4x-12 ≤ 0 (kedua ruas dikali -1 sehingga tandanya jadi ≤)
Pembuat nolnya adalah
x2-4x-12 = 0
(x-6)(x+2) = 0
x-6 = 0 atau x+2 = 0
x = 6 x = -2
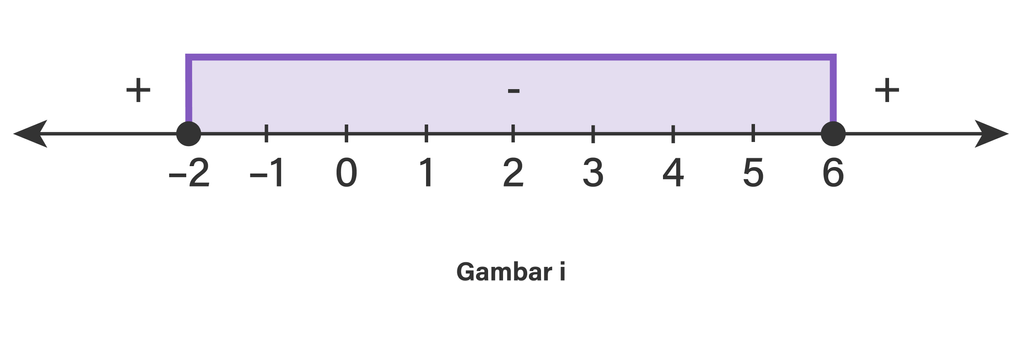
Perhatikan gambar (i) berikut!
Uji titik untuk menentukan tanda pada setiap interval.
x = -5 maka diperoleh hasil berupa bilangan positif.
x = 0 maka diperoleh hasil berupa bilangan negatif.
x = 10 maka diperoleh hasil berupa bilangan positif.
Noktahnya bulat penuh karena tanda pertidaksamaannya ≤.
Karena tandanya ≤, pilih daerah yang negatif.
Sehingga, penyelesaiannya adalah -2≤x≤6.
Langkah 2. Menentukan syarat umerus.
(12+4x) > 0 dan x2 > 0.
(12+4x) > 0
4x > -12
x > -3
Dan,
x2 > 0, maka x∈R.
Sehingga, untuk syarat numerus diperoleh batas x> -3.
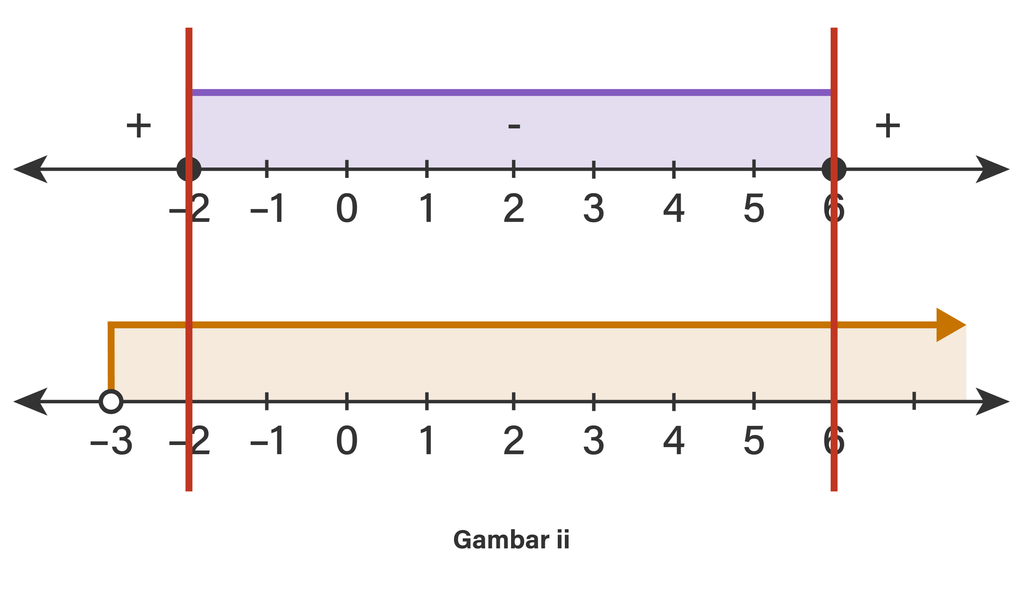
Langkah 3. Menentukan penyelesaian.
Penyelesaiannya adalah irisan dari -2≤x≤6 dan x> -3.
Perhatikan gambar (ii) berikut!
Sehingga, penyelesaiannya adalah -2≤x≤6.
Jadi, jawaban yang benar adalah -2≤x≤6.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



