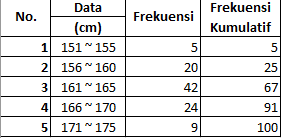
Tentukan nilai Q2, D5, dan P80. Data (cm) frekuensi (151-155) 5 (156-160) 20 (161-165) 42 (166-170) 24 (171-175) 9

Hi Winda S, kakak coba bantu jawab ya. Nilai-nilai yang diminta adalah: Q₂ = 𝟏𝟔𝟑,𝟒𝟕 𝐜𝐦 D₅ = 𝟏𝟔𝟑,𝟒𝟕 𝐜𝐦 P₈₀ = 𝟏𝟔𝟖,𝟐𝟏 𝐜𝐦 Untuk memperoleh nilai-nilai jawaban di atas digunakan rumus statistika: -Berdasarkan soal bisa ditentukan panjang kelas dan jumlah frekuensi: Panjang kelas = c = banyaknya data dalam satu kelas = (155 -151) +1 = 5 (berdasarkan kelas data yang paling atas) Jumlah frekuensi = n = 5 +20 +42 +24 +9 = 100 -Rumus Kuartil untuk Data Kelompok Qᵢ = Tbᵢ +(((i/4)n – Fᵢ)/fᵢ)c dengan Qᵢ = Posisi Kuartil (Q₁, Q₂, Q₃) Tbᵢ = Tepi bawah kuartil ke-i Fᵢ = Jumlah frekuensi sebelum frekuensi kuartil ke-i fᵢ = Frekuensi kuartil ke-i n = Jumlah seluruh frekuensi c = Panjang interval kelas Kuartil terdiri dari: Q₁ = Kuartil Bawah = ¼ dari Total Data Q₂ = Kuartil Tengah/Median = ½ dari Total Data Q₃ = Kuartil Atas = ¾ dari Total Data Untuk menentukan nilai Q₂: Q₂ = Tb₂ +(((2/4)n -F₂)/f₂)c Letak Q₂ berada di ½ data, sehingga letaknya ada di: ½ x Jumlah Data = ½ x 100 = data ke-50 Perhatikan tabel pada soal bahwa data ke-50 terletak di kelas ke: 3. (161 ~ 165) dengan 42 data, sehingga: Tb₂ = Tepi bawah kuartil ke-2 = 161 -0,5 = 160,5 F₂ = 5 +20 = 25 f₂ = 42 n = 100 c = 5 maka, Q₂ = Tb₂ +(((2/4)n -F₂)/f₂)c Q₂ = 160,5 +(((2/4)100 -25)/42) x5 Q₂ = 160,5 +((50 -25)/42) x5 Q₂ = 160,5 +(25/42) x5 Q₂ = 160,5 +2,97 Q₂ = 𝟏𝟔𝟑,𝟒𝟕 𝐜𝐦 -Rumus Desil untuk Data Kelompok Dᵢ = Tbᵢ +(((i/10)n – Fᵢ)/fᵢ)c dengan Dᵢ = Posisi Desil (D₁, D₂, ...D₅, ...D₁₀) Perbedaan Desil dan Kuartil adalah, Kuartil membagi data menjadi 3 bagian (bawah, tengah dan atas) Desil membagi data menjadi 10 bagian (D₁, D₂, ...D₅, ...D₁₀) Untuk menentukan nilai D₅: D₅ = Tb₅ +(((5/10)n -F₅)/f₅)c Letak D₅ berada di 5/10 data, sehingga letaknya ada di: 5/10 x 100 = data ke-50 Sesuai dengan perhitungan sebelumnya data ke-50 terletak di kelas ke: 3. (161 ~ 165) dengan 42 data, sehingga: Tb₅ = 160,5 F₅ = 5 +20 = 25 f₅ = 42 n = 100 c = 5 maka, D₅ = Tb₅ +(((5/10)n -F₅)/f₅)c D₅ = 160,5 +(((5/10)100 -25)/42) x5 D₅ = 𝟏𝟔𝟑,𝟒𝟕 𝐜𝐦 Ternyata Q₂ dan D₅ memiliki nilai yang sama karena merupakan nilai tengah dari data (2/4 dan 5/10). -Rumus Persentil untuk Data Kelompok Pᵢ = Tbᵢ + (((i/100)n – Fᵢ)/fᵢ)c dengan Pᵢ = Posisi Persentil (P₁, P₂, ...P₈₀, ...D₁₀₀) Persentil membagi data menjadi 100 bagian (P₁, P₂, ...P₈₀, ...D₁₀₀) Untuk menentukan nilai P₈₀: P₈₀ = Tb₈₀ + (((80/100)n – F₈₀)/f₈₀)c Letak P₈₀ berada di 80/100 data, sehingga letaknya ada di: 80/100 x 100 = data ke-80 Perhatikan tabel pada soal bahwa data ke-80 terletak di kelas ke: 4. (166 ~ 170) dengan 24 data, sehingga: Tb₈₀ = 166 -0,5 = 165,5 F₈₀ = 5 +20 +42 = 67 f₈₀ = 24 n = 100 c = 5 maka P₈₀ = Tb₈₀ +(((80/100)n – F₈₀)/f₈₀)c P₈₀ = 165,5 +(((80/100)100 – 67)/24) x5 P₈₀ = 165,5 +((80 -67)/24) x5 P₈₀ = 165,5 +(13/24) x5 P₈₀ = 𝟏𝟔𝟖,𝟐𝟏 𝐜𝐦 Berdasarkan hasil ketiga perhitungan di atas jawabannya ialah: Q₂ = D₅ = 𝟏𝟔𝟑,𝟒𝟕 𝐜𝐦 dan P₈₀ = 𝟏𝟔𝟖,𝟐𝟏 𝐜𝐦 Demikian penjelasan kakak, semoga mudah dipahami ya. Tetap semangat belajar.