FN
Fatima N
28 Juni 2022 15:16
Iklan
FN
Fatima N
28 Juni 2022 15:16
Pertanyaan
Tentukan luas irisan dua lingkaran berikut. b. x² + y² – 2x – 4y + 1 = 0 dan x² + y² – 4x – 2y + 2 = 0
3
1
Iklan
SS
S. SheilaTeacherAssisstant
Mahasiswa/Alumni Universitas Pancasila
29 Juni 2022 10:52
Jawaban terverifikasi
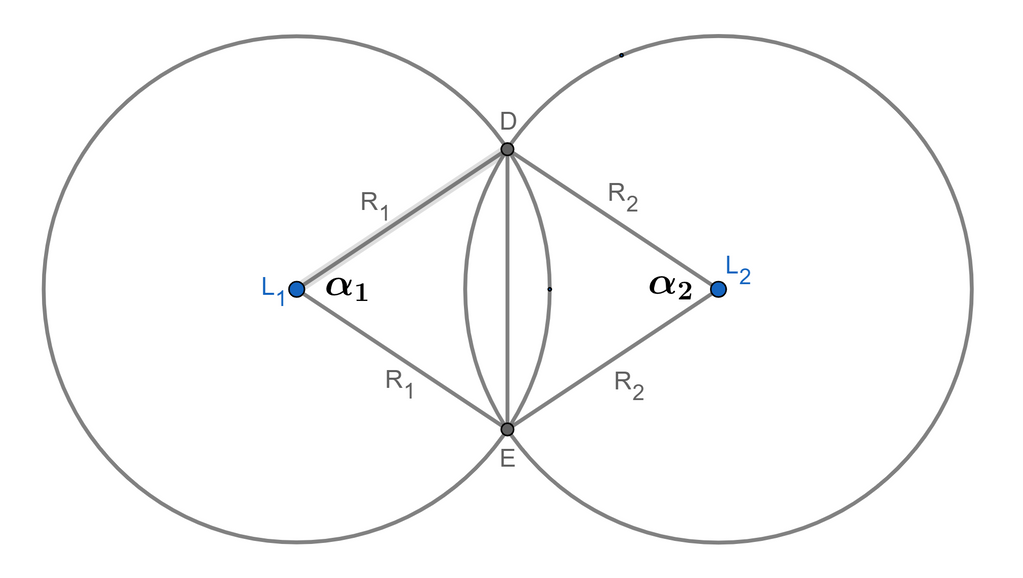
Jawaban yang benar adalah 0,104 satuan luas. Pembahasan: Dalam menentukan luas irisan dua lingkaran, langkah-langkah yang harus dilakukan adalah: 1. Cari titik potong kedua lingkaran. 2. Cari jarak kedua titik tersebut. 3. Cari sudut pusat kedua lingkaran. 4. Cari luas juring dan tembereng kedua lingkaran. 5. Jumlahkan luas kedua tembereng tersebut. Rumus-rumus yang digunakan adalah (lihat gambar): Persamaan umum lingkaran: x² + y² + Ax + By + C = 0 P(-½A, -½B) R = √(¼A² + ¼B² – C) Jarak antara dua titik: √[(x₂ – x₁)² + (y₂ – y₁)²] L juring = (α/360°) × πR² L tembereng = L juring – L segitiga pusat L segitiga pusat (menggunakan Aturan Sinus) = ½R² sin α Mencari α dengan Aturan Cosinus: cos α = (2R² – DE²)/2R² Sehingga, untuk soal berikut: L₁ : x² + y² – 2x – 4y + 1 = 0 P₁[-½ × (-2), -½ × (-4)] = P(1, 2) R₁ = √[¼(-2)² + ¼(-4)² – 1] R₁ = √[¼(4) + ¼(16) – 1] R₁ = √(1 + 4 – 1) R₁ = √4 R₁ = 2 L₂ : x² + y² – 4x – 2y + 2 = 0 P₂[-½ × (-4), -½ × (-2)] = P(2, 1) R₂ = √[¼(-4)² + ¼(-2)² – 2] R₂ = √[¼(16) + ¼(4) – 2] R₂ = √(4 + 1 – 2) R₂ = √3 1. Titik potong kedua lingkaran Pertama eliminasi kedua persamaan lingkaran sehingga diperoleh persamaan: 2x = 2y + 1 atau x = y + ½, kemudian substitusi ke persamaan (1) atau (2) pilih salah satu yang paling mudah. (y + ½)² + y² – (2y + 1) – 4y + 1 = 0 y² + y + ¼ + y² – 2y – 1 – 4y + 1 = 0 2y² – 5y + ¼ = 0 (dikalikan dengan 4) 8y² – 10y + 1 = 0 Karena tidak dapat difaktorkan biasa, gunakan Rumus abc untuk mencari y: y₁₂ = (-b ± √b² – 4ac)/(2a) dengan a = 8, b = -10, c = 1 diperoleh: y₁₂ = {-(-10) ± √[(-10)² – 4(8)(1)]}/(2 × 8) y₁₂ = [10 ± √(100 – 32)]/16 y₁₂ = (10 ± √68)/16 Maka y₁ = (10 + √68)/16 = 1,14. y₂ = (10 – √68)/16 = 0,1. Dengan x = y + ½, diperoleh x₁ = y₁ + ½ = 1,14 + ½ = 1,64 D(1,14 ; 1,64) x₂ = y₂ + ½ = 0,1 + ½ = 0,6 E(0,1 ; 0,6) 2. Jarak DE. DE = √[(0,1 – 1,14)² + (0,6 – 0,64)²] DE = √[(-1,04)² + (-0,04)²] DE = √(1,0816 + 0,0016) DE = √1,0832 DE = 1,04 3. Sudut pusat lingkaran: cos α₁ = (2 · 2² – 1,04²)/(2 × 2²) cos α₁ = (8 – 1,0816)/8 cos α₁ = 6,9184/8 cos α₁ = 0,8648 α₁ = arc cos 0,8648 α₁ = 30,16° cos α₂ = [2(√3)² – 1,04²)/[2 × (√3)²] cos α₂ = (6 – 1,0816)/6 cos α₂ = 4,9184/6 cos α₂ = 0,82 α₂ = arc cos 0,82 α₂ = 34,92° 4. Luas juring dan tembereng: L juring₁ = (α₁/360°) × πR₁² L juring₁ = (30,16°/360°) × 3,14 × 2² L juring₁ = 1,052 satuan luas. L segitiga pusat₁ = ½R₁² sin α₁ L segitiga pusat₁ = ½(2)² sin 30,16° L segitiga pusat₁ = 2 × 0,502 = 1,004 satuan luas. L tembereng₁ = L juring₁ – L segitiga pusat₁ L tembereng₁ = 1,052 – 1,004 = 0,048 satuan luas. L juring₂ = (α₂/360°) × πR₂² L juring₂ = (34,92°/360°) × 3,14 × (√3)² L juring₂ = 0,914 satuan luas. L segitiga pusat₂ = ½R₂² sin α₂ L segitiga pusat₂ = ½(√3)² sin 34,92° L segitiga pusat₂ = 1,5 × 0,572 = 0,858 satuan luas. L tembereng₂ = L juring₂ – L segitiga pusat₂ L tembereng₂ = 0,914 – 0,858 = 0,056 satuan luas. 5. Luas Irisan Kedua Lingkaran L = L tembereng₁ + L tembereng₂ L = 0,048 + 0,056 L = 0,104 satuan luas. Jadi, luas irisan dua lingkaran tersebut adalah 0,104 satuan luas.
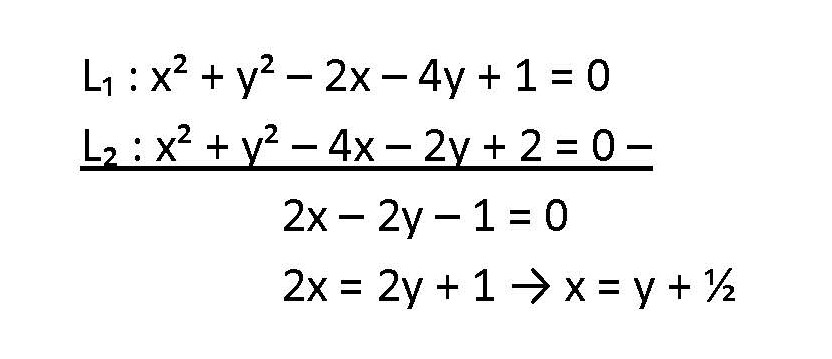
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



