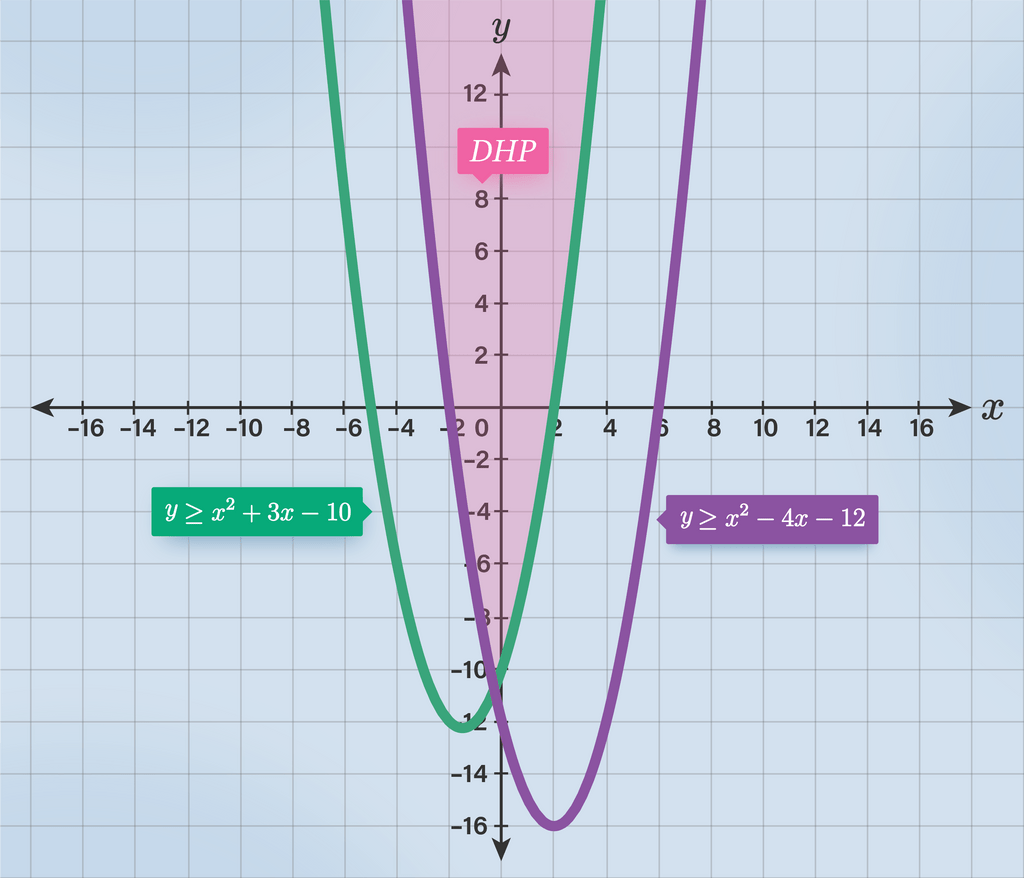
Tentukan himpunan penyelesaian dari: y≥x²−4x−12 y≥x²+3x−10

Halo Teguh S, jawaban untuk soal di atas adalah di bawah ini. Pembahasan: Cara menentukan daerah himpunan penyelesaian sistem pertidaksamaan kuadrat: 1. Ubah tanda pertidaksamaan menjadi tanda persamaan. 2. Gambar masing-masing grafik fungsi kuadrat. 3. Tentukan daerah himpunan penyelesaian dengan titik uji Diketahui sistem pertidaksamaan kuadrat: y ≥ x² − 4x − 12 ...(1) y ≥ x² + 3x − 10 ...(2) Ubah tanda pertidaksamaan menjadi tanda persamaan: y ≥ x² − 4x − 12 y = x² − 4x − 12 Gambar grafik fungsi kuadrat y = x² − 4x − 12: a. Titik potong terhadap sumbu x jika y = 0: x² − 4x − 12 = 0 (x + 2)(x − 6) = 0 x + 2 = 0 x = −2 x − 6 = 0 x = 6 Titik potongnya adalah (−2,0) dan (6,0) b. Titik potong terhadap sumbu y jika x = 0: y = x² − 4x − 12 y = 0² − 4(0) −12 y = −12 Titik potongnya adalah (0,−12) c. Persamaan sumbu simetri dari y = ax² + bx + c: x = -b/2a y = x² − 4x − 12, maka a = 1, b = −4 dan c = −12 sehingga persamaan sumbu simetrinya x = −( −4)/2(1) = 2 d. Titik balik maksimum atau minimum: karena a > 0 maka grafiknya terbuka ke atas sehingga mempunyai titik balik minimum adalah (2, f(2)) y = f(x) = x² − 4x − 12 y = f(2) = 2² − 4(2) − 12 y = f(2) = 4 - 8 - 12 y = f(2) = -16 Jadi, titik balik minimumnya adalah (2, -16) Menentukan daerah penyelesaian y ≥ x² − 4x − 12 dengan titik uji: Ambil titik uji (0,0) di dalam kurva lalu dimasukan ke pertidaksamaan (1): y ≥ x² − 4x − 12 0 ≥ 0² − 4(0) − 12 0 ≥ −12 (Benar) Sehingga daerah penyelesaiannya berada di dalam kurva. Ubah tanda pertidaksamaan menjadi tanda persamaan: y ≥ x² + 3x − 10 y = x² + 3x − 10 Gambar grafik fungsi kuadrat y = x² + 3x − 10: a. Titik potong terhadap sumbu x jika y = 0: x² + 3x − 10 = 0 (x + 5)(x − 2) = 0 x + 5 = 0 x = −5 x − 2 = 0 x = 2 Titik potongnya adalah (−5,0) dan (2,0) b. Titik potong terhadap sumbu y jika x = 0: y = x² + 3x − 10 y = 0² + 3(0) − 10 y = −10 Titik potongnya adalah (0,−10) c. Persamaan sumbu simetri dari y = ax² + bx + c: x = -b/2a y = x² + 3x − 10, maka a = 1, b = 3 dan c = −10 sehingga persamaan sumbu simetrinya x = −3/2(1) = −3/2 d. Titik balik maksimum atau minimum: karena a > 0 maka grafiknya terbuka ke atas sehingga mempunyai titik balik minimum adalah (−3/2, f(−3/2)) y = f(x) = x² + 3x − 10 y = f(−3/2) = (-3/2)² + 3(-3/2) − 10 y = f(−3/2) = (9/4) − (9/2) − 10 y = f(−3/2) = −2,25 - 10 y = f(−3/2) = −12,25 Jadi, titik balik minimumnya adalah (−3/2, −12,25) Menentukan daerah penyelesaian y ≥ x² + 3x − 10 dengan titik uji: Ambil titik uji (0,0) di dalam kurva lalu dimasukan ke pertidaksamaan (2): y ≥ x² + 3x − 10 0 ≥ 0² + 3(0) − 10 0 ≥ −10 (Benar) Sehingga daerah penyelesaiannya berada di dalam kurva. Jadi, daerah himpunan penyeleasaian di atas yaitu