Tentukan fungsi objektif, fungsi kendala, dan nilai optimum dari masalah program linier berikut. Seorang nutrisionis rumah sakit akan membuat menu makanan yang mengandung sekurang kurangnya 72 gram lemak, 48 gram protein, 100 karbohidrat, dan 300 miligram natrium. Tiap 100 gram bahan makanan A mengandung 6 gram lemak, 8 gram protein, 50 gram karbohidrat, dan 20 miligram natrium. Sedangkan bahan makanan B mengandung 12 gram lemak, 4 gram protein, 5 gram karbohidrat, dan 100 miligram natrium. Jika diketahui harga per pack (100 gram) bahan makanan A adalah Rp. 2.500 dan bahan makanan B adalah Rp. 3.000. Hitunglah berapa banyak penggunaan bahan makanan A dan B agar biaya menu makanan semurah mungkin.

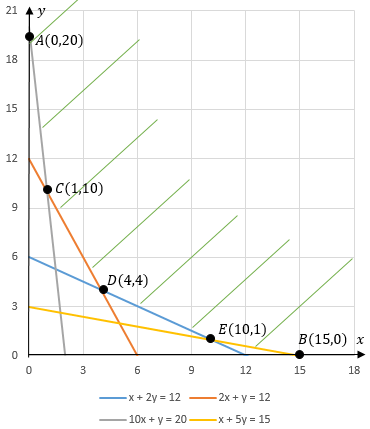
Jawaban yang benar adalah 4 bahan makanan A dan 4 bahan makanan B. Ingat! Untuk membuat model matematika yaitu dengan memisalkan variabel yang akan digunakan, lalu membuat fungsi kendala berupa sistem pertidaksamaan serta membuat fungsi tujuan. Lalu, gambar daerah penyelesaiannya. Untuk menentukan daerah penyelesaian yaitu dengan mengubah pertidaksamaan menjadi persamaan, lalu gambar garisnya, dan cari daerah yang memenuhi sistem pertidaksamaan tersebut. Misalkan x : banyak bahan makanan A y : banyak bahan makanan B Karena semua kendala merupakan kebutuhan, maka digunakan pertidaksamaan ≥. Kendala kebutuhan lemak : 6x + 12y ≥ 72 (kedua ruas dibagi 6) x + 2y ≥ 12 Kendala kebutuhan protein : 8x + 4y ≥ 48 (kedua ruas dibagi 4) 2x + y ≥ 12 Kendala kebutuhan karbohidrat : 50x + 5y ≥ 100 (kedua ruas dibagi 5) 10x + y ≥ 20 Kendala kebutuhan natrium : 20x + 100y ≥ 300 (kedua ruas dibagi 20) x + 5y ≥ 15 Ditambahkan juga kendala non negatif karena banyak bahan makanan tidak mungkin negatif, maka: x≥0, y≥0 Jika diketahui harga per pack (100 gram) bahan makanan A adalah Rp2.500,00 dan bahan makanan B adalah Rp3.000,00, maka fungsi tujuannya adalah f(x, y) = 2.500 x + 3.000 y Jadi, model matematika nya adalah sebagai berikut f(x, y) = 2.500 x + 3.000 y dengan kendala x + 2y ≥ 12 2x + y ≥ 12 10x + y ≥ 20 x + 5y ≥ 15 x≥0, y≥0 Ubah pertidaksamaan menjadi persamaan Pertama, gambar garis x + 2y = 12. Titik potong garis dengan sumbu y, substitusi x=0 0 + 2y = 12 2y = 12 y = 6 (0,6) Titik potong garis dengan sumbu x, substitusi y=0 x + 2(0) = 12 x = 12 (12,0) Uji titik: Pilih (0,0) 0+2(0) ... 12 0 ≤ 12 Karena x + 2y ≥ 12 maka yang diarsir adalah daerah yang tidak memuat titik (0,0). Kedua, gambar garis 2x + y = 12. Titik potong garis dengan sumbu y, substitusi x=0 2(0) + y = 12 y = 12 (0,12) Titik potong garis dengan sumbu x, substitusi y=0 2x + 0 = 12 x = 6 (6,0) Uji titik: Pilih (0,0) 2(0)+0 ... 12 0 ≤ 12 Karena 2x + y ≥ 12 maka yang diarsir adalah daerah yang tidak memuat titik (0,0). Ketiga, gambar garis 10x + y = 20. Titik potong garis dengan sumbu y, substitusi x=0 10(0) + y = 20 y = 20 (0,20) Titik potong garis dengan sumbu x, substitusi y=0 10x + 0 = 20 x = 2 (2,0) Uji titik: Pilih (0,0) 10(0)+0 ... 20 0 ≤ 20 Karena 10x + y ≥ 20 maka yang diarsir adalah daerah yang tidak memuat titik (0,0). Keempat, gambar garis x + 5y = 15. Titik potong garis dengan sumbu y, substitusi x=0 0 + 5y = 15 y = 3 (0,3) Titik potong garis dengan sumbu x, substitusi y=0 x + 5(0) = 15 x = 15 (15,0) Uji titik: Pilih (0,0) 0+5(0) ... 15 0 ≤ 15 Karena x + 5y ≥ 15 maka yang diarsir adalah daerah yang tidak memuat titik (0,0). Karena x≥0, y≥0 maka daerah yang diarsir adalah daerah di kuadran I. Lalu, gambar daerah penyelesaiannya. Titik sudut pada daerah yang diarsir adalah A(0,20), B(15,0), titik potong antara 2x + y = 12 dan 10x + y = 20, titik potong antara x + 2y = 12 dan 2x + y = 12, serta titik potong antara x + 2y = 12 dan x + 5y = 15. Titik potong 2x + y = 12 10x + y = 20 __________- -8x = -8 x = 1 Substitusi x = 1 ke 2x + y = 12 2(1) + y = 12 2 + y = 12 y = 10 Diperoleh C(1,10) Titik potong x + 2y = 12|x1| 2x + 4y = 24 2x + y = 12|x2| 2x + y = 12 .......................___________- ........................3y = 12 ........................y = 4 Substitusi y = 4 ke 2x + y = 12 2x + 4 = 12 2x = 8 x = 4 Diperoleh D(4,4) Titik potong x + 2y = 12 x + 5y = 15 ___________- -3y = -3 y = 1 Substitusi y = 1 ke x + 2y = 12 x + 2(1) = 12 x + 2 = 12 x = 10 Diperoleh E(10,1) Cek pada fungsi tujuannya Untuk A(0,20) diperoleh f(0,20) = 2.500 (0) + 3.000 (20) = 0 + 60.000 = 60.000 Untuk B(15,0) diperoleh f(15,0) = 2.500 (15) + 3.000 (0) = 37.500 + 0 = 37.500 Untuk C(1,10) diperoleh f(1,10) = 2.500 (1) + 3.000 (10) = 2.500 + 30.000 = 32.500 Untuk D(4,4) diperoleh f(4,4) = 2.500 (4) + 3.000 (4) = 10.000 + 12.000 = 22.000 Untuk E(10,1) diperoleh f(10,1) = 2.500 (10) + 3.000 (1) = 25.000 + 3.000 = 28.000 Jadi, banyak penggunaan bahan makanan A dan B agar biaya menu makanan semurah mungkin adalah 4 bahan makanan A dan 4 bahan makanan B.