Raden R
05 Agustus 2022 05:42
Iklan
Raden R
05 Agustus 2022 05:42
Pertanyaan
Tentukan daerah penyelesaian dari pertidaksamaan berikut: b. 4x+5y < 20 dan x+2y ≥ 2
2
2
Iklan
Y. Frando
09 Oktober 2022 11:42
<p>Jawabannya adalah daerah himpunan penyelesaian seperti gambar di bawah.</p><p> </p><p>Diketahui:</p><p>4x+5y < 20</p><p>x+2y ≥ 2</p><p> </p><p>Ditanya:</p><p>Daerah penyelesaian = ...?</p><p><br>Jawab:</p><p>Konsep yang kita gunakan adalah program linier. Cara menentukan himpunan penyelesaian dari pertidaksamaan yang diberikan adalah sebagai berikut:</p><p>a. Tentukanlah titik potong pada sumbu x (saat y = 0)</p><p>b. Tentukanlah titik potong pada sumbu y (saat x = 0)</p><p>c. Jika terdapat dua atau lebih pertidaksamaan, maka cari kemungkinan titik potong keduanya .</p><p>d. Kemudian tentukan daerah himpunan penyelesaiannya dengan mengarsir daerah yang sesuai dengan tanda ketidaksamaan.</p><p> </p><p>Berdasarkan informasi soal telah diberikan dua pertidaksamaan. Maka analisis masing-masing pertidaksamaan.</p><p>1. Titik potong pada sumbu x (saat y = 0)</p><p>4x + 5y = 20</p><p>4x + 5(0) = 20</p><p>x = 20/4</p><p>x = 5.</p><p>Titik (5, 0).</p><p> </p><p>Titik potong pada sumbu y (saat x = 0)</p><p>4x + 5y = 20</p><p>4(0) + 5y = 20</p><p>y = 20/5</p><p>y = 4.</p><p>Titik (0, 4).</p><p> </p><p>2. Titik potong pada sumbu x (saat y = 0)</p><p>x + 2y = 2</p><p>x + 2(0) = 2</p><p>x = 2.</p><p>Titik (2, 0).</p><p> </p><p>Titik potong pada sumbu y (saat x = 0)</p><p>x + 2y = 2</p><p>0 + 2y = 2</p><p>y = 2/2</p><p>y = 1.</p><p>Titik (0, 1).</p><p> </p><p>3. Selesaikan kedua pertidaksamaan maka diperoleh:</p><p>4x + 5y = 20 (kalikan 1) ---> 4x + 5y = 20</p><p>x + 2y = 2 (kalikan 4) -------> 4x + 8y = 8</p><p> </p><p>4x + 5y = 20</p><p>4x + 8y = 8</p><p>---------------- -</p><p>-3y = 12</p><p>y = -4.</p><p> </p><p>Dari persamaan (1) diperoleh:</p><p>4x + 5y = 20</p><p>4x + 5(-4) = 20</p><p>4x = 20 + 20</p><p>x = 10.</p><p>Titik (10, -4).</p><p> </p><p>Gambarkan titik-titik yang diperoleh ke dalam diagram kartesius yang sama. Lalu, uji titik (0, 0) untuk menentukan daerah himpunan penyelesaian pada masing-masing pertidaksamaan.</p><p> </p><p>(a). 4x + 5y < 20</p><p>4(0) + 5 (0) < 20</p><p>0 < 20.</p><p>Karena benar, maka daerah himpunan penyelesaian mendekati titik (0, 0). Lihat pada grafik yang arsiran berwarna merah.</p><p> </p><p>(b). x + 2y ≥ 2</p><p>0 + 2(0) ≥ 2</p><p>0 ≥ 2. </p><p>Karena salah, maka daerah himpunan penyelesaian menjauhi titik (0, 0). Lihat pada grafik yang arsiran berwarna biru.</p><p> </p><p>Sehingga daerah yang terkena arsiran dua kali merupakan daerah himpunan penyelesaian seperti gambar di bawah.</p><p> </p><p>Jadi, daerah himpunan penyelesaian dari pertidaksamaan tersebut ditunjukkan seperti gambar di bawah.</p>
Jawabannya adalah daerah himpunan penyelesaian seperti gambar di bawah.
Diketahui:
4x+5y < 20
x+2y ≥ 2
Ditanya:
Daerah penyelesaian = ...?
Jawab:
Konsep yang kita gunakan adalah program linier. Cara menentukan himpunan penyelesaian dari pertidaksamaan yang diberikan adalah sebagai berikut:
a. Tentukanlah titik potong pada sumbu x (saat y = 0)
b. Tentukanlah titik potong pada sumbu y (saat x = 0)
c. Jika terdapat dua atau lebih pertidaksamaan, maka cari kemungkinan titik potong keduanya .
d. Kemudian tentukan daerah himpunan penyelesaiannya dengan mengarsir daerah yang sesuai dengan tanda ketidaksamaan.
Berdasarkan informasi soal telah diberikan dua pertidaksamaan. Maka analisis masing-masing pertidaksamaan.
1. Titik potong pada sumbu x (saat y = 0)
4x + 5y = 20
4x + 5(0) = 20
x = 20/4
x = 5.
Titik (5, 0).
Titik potong pada sumbu y (saat x = 0)
4x + 5y = 20
4(0) + 5y = 20
y = 20/5
y = 4.
Titik (0, 4).
2. Titik potong pada sumbu x (saat y = 0)
x + 2y = 2
x + 2(0) = 2
x = 2.
Titik (2, 0).
Titik potong pada sumbu y (saat x = 0)
x + 2y = 2
0 + 2y = 2
y = 2/2
y = 1.
Titik (0, 1).
3. Selesaikan kedua pertidaksamaan maka diperoleh:
4x + 5y = 20 (kalikan 1) ---> 4x + 5y = 20
x + 2y = 2 (kalikan 4) -------> 4x + 8y = 8
4x + 5y = 20
4x + 8y = 8
---------------- -
-3y = 12
y = -4.
Dari persamaan (1) diperoleh:
4x + 5y = 20
4x + 5(-4) = 20
4x = 20 + 20
x = 10.
Titik (10, -4).
Gambarkan titik-titik yang diperoleh ke dalam diagram kartesius yang sama. Lalu, uji titik (0, 0) untuk menentukan daerah himpunan penyelesaian pada masing-masing pertidaksamaan.
(a). 4x + 5y < 20
4(0) + 5 (0) < 20
0 < 20.
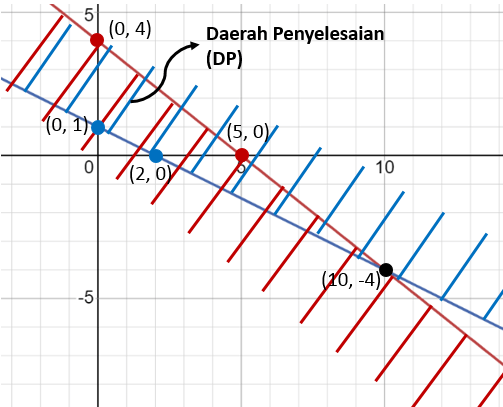
Karena benar, maka daerah himpunan penyelesaian mendekati titik (0, 0). Lihat pada grafik yang arsiran berwarna merah.
(b). x + 2y ≥ 2
0 + 2(0) ≥ 2
0 ≥ 2.
Karena salah, maka daerah himpunan penyelesaian menjauhi titik (0, 0). Lihat pada grafik yang arsiran berwarna biru.
Sehingga daerah yang terkena arsiran dua kali merupakan daerah himpunan penyelesaian seperti gambar di bawah.
Jadi, daerah himpunan penyelesaian dari pertidaksamaan tersebut ditunjukkan seperti gambar di bawah.
· 0.0 (0)
Iklan
Nur N
12 Juni 2024 13:11
Gambarla daerah penyelesaian dari tidak persamaan 5y-4×←20
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



