Radhelia K
27 Februari 2023 03:36
Iklan
Radhelia K
27 Februari 2023 03:36
Pertanyaan
Tentukan akar-akar rasional dari setiap persamaan berikut. d. 6x^3 + 11x^2 - x - 6 = 0
3
1
Iklan
H. Eka
Mahasiswa/Alumni Universitas Pendidikan Indonesia
09 Maret 2023 03:21
<p>Jawaban yang benar adalah x = -1, x = -3/2, dan x = 2/3.</p><p> </p><p>Ingat!</p><p>Misalkan diketahui persamaan suku banyak:</p><p>ax<sup>n</sup> + cx<sup>n-1</sup> + c<sub>1</sub>x<sup>n-2</sup> + ... + c<sub>n-1</sub>x + b = 0</p><p>Langkah-langkah menentukan akar-akarnya:</p><p>1) Menentukan akar-akar rasional yang mungkin diperoleh dari pembagian: (faktor b/faktor a). Jika a = 1, akar-akar yang mungkin adalah faktor dari b.</p><p>2) Dari akar-akar yang mungkin tersebut, kita substitusi ke bentuk suku banyaknya. Jika hasil substitusi sama dengan nol, maka bilangan tersebut merupakan akar pertamanya. </p><p>3) Dari akar-akar yang diperoleh dari langkah 2, kita gunakan cara Horner untuk menentukan hasil pembagiannya.</p><p> </p><p>Penyelesaian:</p><p>Diketahui 6x^3 + 11x^2 - x - 6 = 0 sehingga a = 6 dan b = -6.</p><p>Akar-akar yang mungkin dari (faktor -6/faktor 6), yaitu ±1, ±2, ±3, ±6, ±1/3, ±1/2, ±2/3, ±3/2.</p><p>Untuk x = -1</p><p>f(x) = 6x<sup>3</sup> + 11x<sup>2</sup> - x - 6</p><p>f(-1) = 6.(-1)<sup>3</sup> + 11.(-1)<sup>2</sup> - (-1) - 6</p><p>f(-1) = -6 + 11 + 1 - 6</p><p>f(-1) = 0</p><p>Karena f(-1) = 0 sehingga x = -1 merupakan salah satu akar rasionalnya.</p><p> </p><p>Dengan cara horner seperti pada gambar di bawah (REQUEST GAMBAR), diperoleh faktor persamaan polinomial sebagai berikut.</p><p>6x<sup>3</sup> + 11x<sup>2</sup> - x - 6 = 0</p><p>(x + 1)(6x<sup>2</sup>+5x-6) = 0</p><p>(x + 1)(2x+3)(3x-2) = 0</p><p>x = -1 atau x = -3/2 atau x = 2/3.</p><p> </p><p>Jadi, akar-akar rasional dari persamaan tersebut adalah x = -1, x = -3/2, dan x = 2/3.</p>
Jawaban yang benar adalah x = -1, x = -3/2, dan x = 2/3.
Ingat!
Misalkan diketahui persamaan suku banyak:
axn + cxn-1 + c1xn-2 + ... + cn-1x + b = 0
Langkah-langkah menentukan akar-akarnya:
1) Menentukan akar-akar rasional yang mungkin diperoleh dari pembagian: (faktor b/faktor a). Jika a = 1, akar-akar yang mungkin adalah faktor dari b.
2) Dari akar-akar yang mungkin tersebut, kita substitusi ke bentuk suku banyaknya. Jika hasil substitusi sama dengan nol, maka bilangan tersebut merupakan akar pertamanya.
3) Dari akar-akar yang diperoleh dari langkah 2, kita gunakan cara Horner untuk menentukan hasil pembagiannya.
Penyelesaian:
Diketahui 6x^3 + 11x^2 - x - 6 = 0 sehingga a = 6 dan b = -6.
Akar-akar yang mungkin dari (faktor -6/faktor 6), yaitu ±1, ±2, ±3, ±6, ±1/3, ±1/2, ±2/3, ±3/2.
Untuk x = -1
f(x) = 6x3 + 11x2 - x - 6
f(-1) = 6.(-1)3 + 11.(-1)2 - (-1) - 6
f(-1) = -6 + 11 + 1 - 6
f(-1) = 0
Karena f(-1) = 0 sehingga x = -1 merupakan salah satu akar rasionalnya.
Dengan cara horner seperti pada gambar di bawah (REQUEST GAMBAR), diperoleh faktor persamaan polinomial sebagai berikut.
6x3 + 11x2 - x - 6 = 0
(x + 1)(6x2+5x-6) = 0
(x + 1)(2x+3)(3x-2) = 0
x = -1 atau x = -3/2 atau x = 2/3.
Jadi, akar-akar rasional dari persamaan tersebut adalah x = -1, x = -3/2, dan x = 2/3.
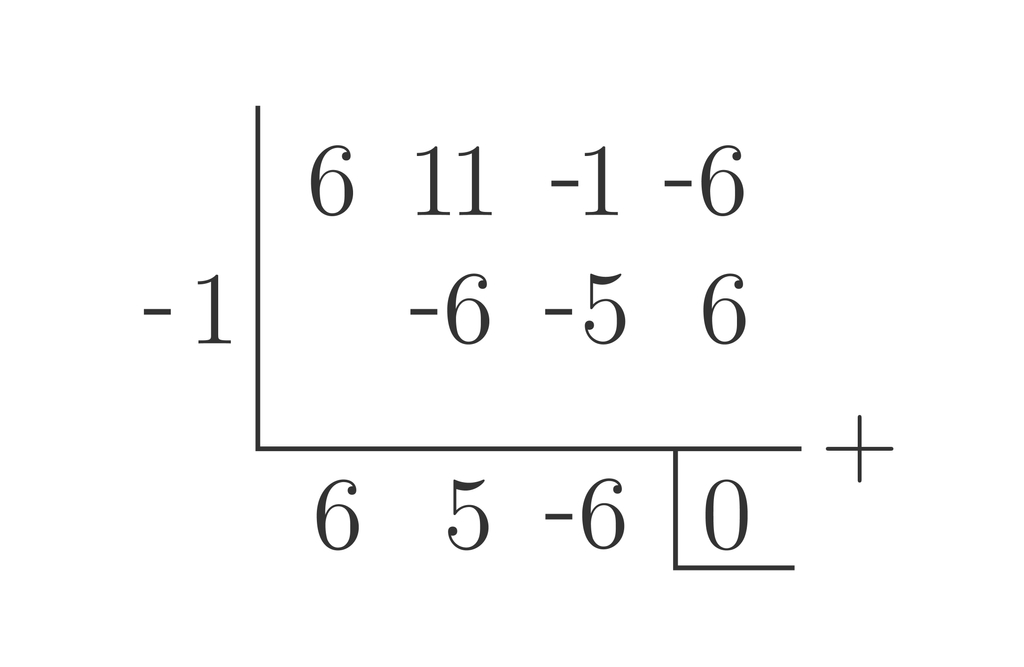
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



