MM
Meta M
09 Januari 2022 15:03
Iklan
MM
Meta M
09 Januari 2022 15:03
Pertanyaan
Suatu perusahaan ingin pindah kantor dan akan mengangkut barang-barangnya yang terdiri dari 480 kardus dan 352 box plastik dengan menyewa 2 jenis kendaraan, yaitu mobil bak dan truk. Mobil bak dapat mengangkut paling sedikit 40 kardus dan 16 box plastik. Truk dapat mengangkut paling sedikit 30 kardus dan 32 peti. Jika sewa untuk mobil bak Rp100.000,00 dan truk Rp150.000,00 sekali jalan. Biaya minimum untuk mengangkut barang-barang tersebut adalah ....
10
2
Iklan
OA
O. Andrianto
16 Januari 2022 14:11
Jawaban terverifikasi
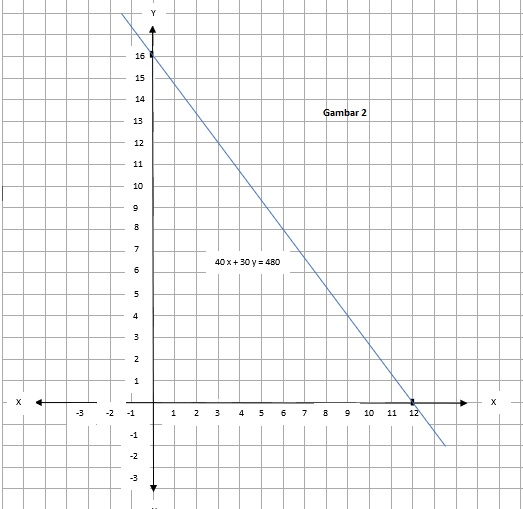
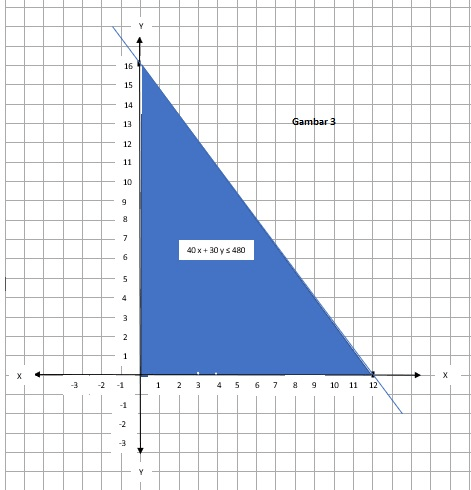
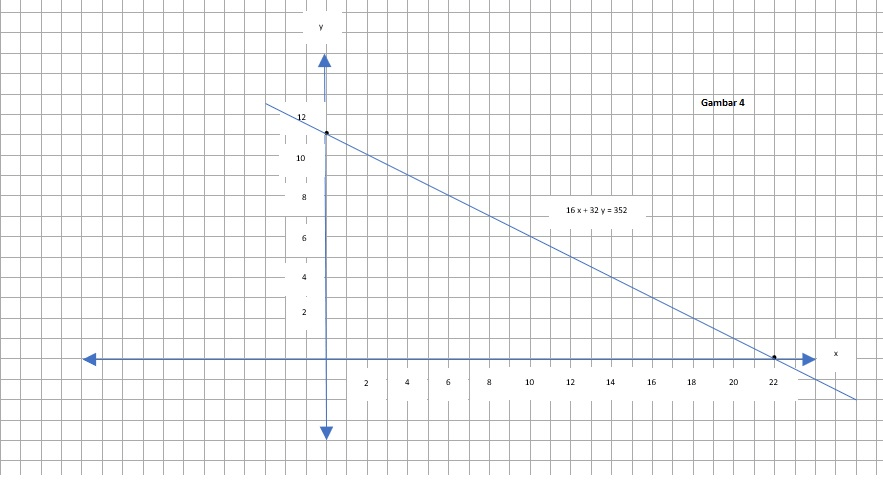
Halo Meta M kaka bantu jawab ya, biaya minimum untuk mengangkut 480 kardus dan 352 box plastik adalah Rp1.200.000 diketahui : - perusahaan ingin mengangkut 480 kardus dan 352 box plastik - mobil bak dapat mengangkut paling sedikit 40 kadrus dan 16 box plastik - truk dapat mengangkut paling sedikit 30 kardus dan 32 box plastik pembahasan : 1. kita asumsikan, lihat gambar (1) - mobil bak = x - truk = y 2. kita buat variable pertidaksamaan dari soal diatas, yaitu : a. 40 x + 30 y ≤ 480 b. 16 x + 32 y ≤352 3. kita gambarkan pertidaksamaan 40 x + 30 y ≤ 480, dengan langkah sebagai berikut : a. kita buat menjadi persamaan terlebih dahulu, yaitu : 40 x + 30 y ≤ 480 b. kita tentukan titik potong 40 x + 30 y = 480, yaitu : - jika x = 0, maka : 40 x + 30 y = 480 40 (0) + 30 y = 480 0 + 30 y = 480 y = 16 titik potongnya (0,16) - jika y = 0, maka : 40 x + 30 y = 480 40 x + 30 (0) = 480 40 x + 0 = 480 x = 12 titik potongnya (12,0) c. kita gambarkan, dengan titik potong {(0,16) dan (12,0)}, lihat gambar (2) d. Uji titik dengan persamaan 40 x + 30 y ≤ 480, dengan titik (1,1), dan (12,2). - titik (1,1) maka : 40 x + 30 y ≤ 480 40 (1) + 30 (1) ≤ 480 40 + 70 ≤ 480 70 ≤ 480 (uji titik benar) - titik (12, 2) maka : 40 x + 30 y ≤ 480 40 (12) + 30 (2) ≤ 480 480 + 60 ≤ 480 540 ≤ 480 (uji titik salah) e.maka kita arsir warna biru dan bisa diliat pada gambar (3) 4. kita gambarkan pertidaksamaan 16 x + 32 y ≤352, dengan langkah sebagai berikut : a. kita buat menjadi persamaan terlebih dahulu, yaitu : 16 x + 32 y = 352 b. kita tentukan titik potong 16 x + 32 y = 352, yaitu : - jika x = 0, maka : 16 x + 32 y = 352 16 (0) + 32 y = 352 0 + 32 y = 352 y = 11 titik potongnya (0,11) - jika y = 0, maka : 16 x + 32 y = 352 16 x + 32 (0) = 352 16 x + 0 = 352 x = 22 titik potongnya (22,0) c. kita gambarkan, dengan titik potong {(0,11) dan (22,0)}, lihat gambar (4) d. Uji titik dengan persamaan 16 x + 32 y ≤352, dengan titik (1,1), dan (22,2). - titik (1,1) maka : 16 x + 32 y ≤352 16 (1) + 32 (1) ≤352 16 + 32 ≤ 352 48 ≤ 352 (uji titik benar) - titik (22, 2) maka : 16 x + 32 y ≤352 16 (22) + 32 (2) ≤352 352 + 64 ≤ 352 416 ≤ 352 (uji titik salah) e.maka kita arsir warna hijau dan bisa diliat pada gambar (5)

Lihat 1 lainnya
· 4.8 (6)
X-
X -
01 Oktober 2022 04:30
Lebih dari kak
Iklan
OA
O. Andrianto
16 Januari 2022 14:48
Jawaban terverifikasi
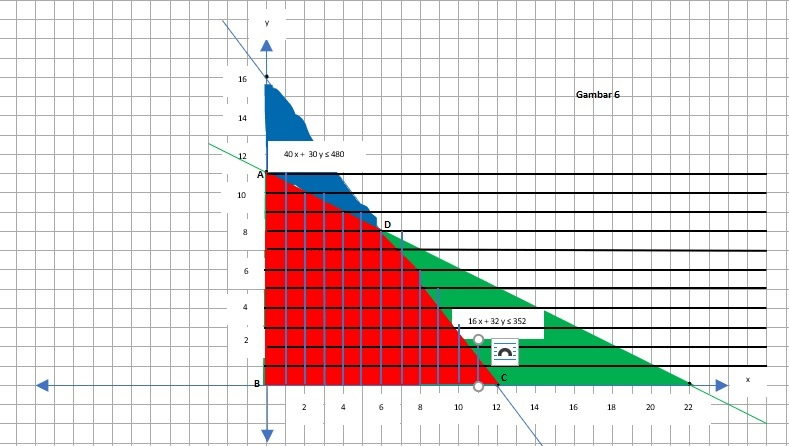
5. kita gabungkan gambar (3) dan (5) menjadi gambar (6), sehingga didapatkan titiknya yang diarsir warna merah, maka didapatkan daerah himpunan penyelesaiannya (DHP), yaitu : - titik A (0,11) - titik B (0,0) - titik C (12,0) - titik D (... , ...) kita mencari titik D dengan menggunakan eliminasi dan substitusi pada persamaan 40 x + 30 y = 480 dan 16 x + 32 y = 352 a. metode eliminasi, kita eliminasikan variabel x, yaitu 40 x + 30 y = 480 | x 2| 16 x + 32 y = 352 | x 5| 80 x + 60 y = 960 80 x + 160 y = 1760 ------------------------- (-) -100 y = -800 y = - 800 / - 100 = 8 b. kita substitusikan nilai y = 8 , ke persamaan 40 x + 30 y = 480, menjadi : 40 x + 30 (8) = 480 40 x + 240 = 480 40 x = 480 - 240 40 x = 240 x = 240 / 40 = 6 maka titik D, yaitu (6,8) 6. kita cari nilai minimum f(x,y)=100.000x+150.000y, dengan nilai titik yang sudah didapatkan : f(0,11) = 100.000x+150.000y f(0,11) = 100.000 (0) +150.000 (11) = f(0,11) = 0 + 1.650.000 = Rp1.650.000 f(0,0) = 100.000x+150.000y f(0,0) = 100.000 (0) + 150.000 (0) f(0,0) = Rp0 f(12,0) = 100.000x+150.000y f(12,0) = 100.000 (12) + 150.000 (0) f(12,0) = 1.200.000 + 0 = Rp1.200.000 f(6,8) = 100.000x+150.000y f(6,8) = 100.000 (6) +150.000 (8) f(6,8) = 600.000 + 1.200.000 = Rp1.800.000 maka biaya minimum untuk mengangkut barang 480 kardus dan 352 peti adalah Rp1.200.000, terima kasih sudah menjawab, semoga membantu ya
· 5.0 (4)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



