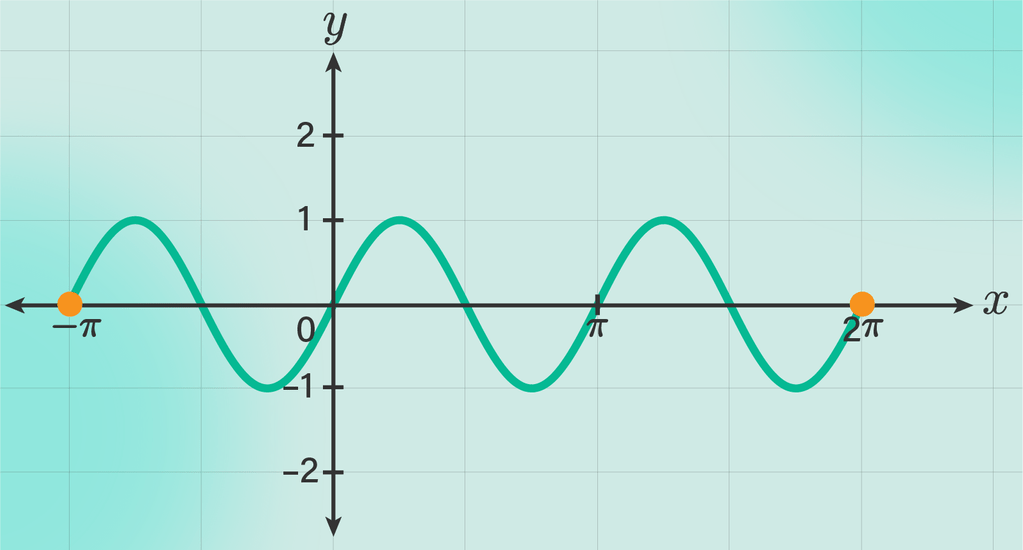
Sketsa grafik berikut pada [-π,2π] y = sin 2x

Question

Jawaban yang benar adalah seperti pada gambar terlampir.

Ingat!

π = 180°

sin (−𝞪) = −sin 𝞪

Konsep sudut berelasi:

sin (360° + 𝞪) = sin 𝞪
Langkah-langkah menggambar grafik
‣Tentukan beberapa titik yang dilalui grafik
‣Hubungkan titik-titik tersebut

Berdasarkan soal, diketahui:

y = sin 2x pada [−π, 2π]

Akan dibuat grafik dengan substitusi beberapa nilai x ∈ [−π, 2π] diperoleh sebagai berikut:

Untuk x = −π = −180°

y = sin 2x

y = sin (2 · −180°)

y = sin (−360°)

y = −sin 360°

y = 0
Diperoleh titik (−π, 0)

Untuk x = −¾π = −135°

y = sin 2x

y = sin (2 · −135°)

y = sin (−270°)

y = −sin 270°

y = −(−1)

y = 1
Diperoleh titik (−¾π, 1)

Untuk x = −½π = −90°

y = sin 2x

y = sin (2 · −90°)

y = sin (−180°)

y = −sin 180°

y = 0
Diperoleh titik (−½π, 0)

Untuk x = −¼π = −45°

y = sin 2x

y = sin (2 · −45°)

y = sin (−90°)

y = −sin 90°

y = −1
Diperoleh titik (−¼π, −1)

Untuk x = 0

y = sin 2x

y = sin (2 · 0°)

y = sin 0°

y = 0
Diperoleh titik (0, 0)

Untuk x = ¼π = 45°

y = sin 2x

y = sin (2 · 45°)

y = sin 90°

y = 1
Diperoleh titik (¼π, 1)

Untuk x = ½π = 90°

y = sin 2x

y = sin (2 · 90°)

y = sin 180°

y = 0
Diperoleh titik (½π, 0)

Untuk x = ¾π = 135°

y = sin 2x

y = sin (2 · 135°)

y = sin 270°

y = −1
Diperoleh titik (¾π, −1)

Untuk x = π = 180°

y = sin 2x

y = sin (2 · 180°)

y = sin 360°

y = 0
Diperoleh titik (π, 0)

Untuk x = ⁵∕₄π = 225°

y = sin 2x

y = sin (2 · 225°)

y = sin 450°

y = sin (360° + 90°)

y = sin 90°

y = 1
Diperoleh titik (⁵∕₄π, 1)

Untuk x = ³∕₂π =270°

y = sin 2x

y = sin (2 · 270°)

y = sin 540°

y = sin (360° + 180°)

y = sin 180°

y = 0
Diperoleh titik ( ³∕₂π, 0)

Untuk x = ⁷∕₄π = 315°

y = sin 2x

y = sin (2 · 315°)

y = sin 630°

y = sin (360° + 270°)

y = sin 270°

y = −1
Diperoleh titik (⁷∕₄π, −1)

Untuk x = 2π = 360°

y = sin 2x

y = sin (2 · 360°)

y = sin 720°

y = sin (360° + 360°)

y = sin 360°

y = 0
Diperoleh titik (2π, 0)

Gambar titik-titik pada bidang kartesius hubungkan menjadi sebuah grafik. Sehingga diperoleh grafiknya seperti pada gambar terlampir.

Jadi, grafik fungsi y = sin 2x pada [−π, 2π] adalah seperti pada gambar terlampir.

Semoga membantu ya😊

Sketsa grafik berikut pada [-π,2π] y = sin 2x

Mau pemahaman lebih dalam untuk soal ini?

Pertanyaan serupa