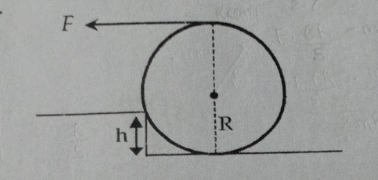
Silinder pejal homogen bermassa m dan berjari - jari R berada pada lantai datar. Silinder itu hendak dinaikkan melewati anak tangga setinggi h dengan cara ditarik dengan gaya F seperti pada gambar. Jika h = R/5 maka besar percepatan sudut sesaat pusat massa silinder adalah .... a. (2mF+g)/R b. (2mF – g)/R c. (F+5mR)/mg d. (6F – 2mg)/5mR e. (6F + 2mg)/5mR

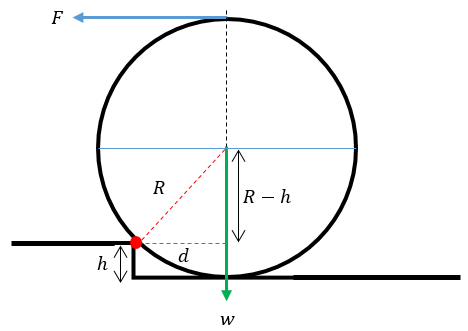
Jawaban yang benar adalah 3 (6F - 2mg) / (5mR), tidak ada pilihan yang sesuai. Diketahui: Silinder pejal (I = 1/2 mR²) Massa = m Jari-jari = R h = R/5 Gaya tarik = F Percepatan gravitasi = g Ditanya: α = ...? Jawab: Konsep yang kita gunakan adalah dinamika rotasi. Ketika benda tegar berotasi, maka terdapat momen gaya yang menyebabkan benda berotasi dan sekaligus bertranslasi. Rumus yang dapat digunakan adalah hukum II Newton dan hubungan antara momen gaya dengan momen inersia. (a). Hukum II Newton: ΣF = m x a. (b). Relasi momen gaya dengan momen inersia: Στ = I x α ---> dimana α = a/R. Keterangan: ΣF = resultan gaya (N) m = massa benda (kg) a = percepatan linier (m/s²) Στ = resultan momen gaya (Nm) I = momen inersia (kg m²) α = percepatan sudut (rad/s²) R = jari-jari benda (m). Berdasarkan gambar diagram gaya yang diberikan pada foto di bawah, pusat rotasi terletak pada titik merah, tempat dimana silinder pejal tepat terangkat. Maka persamaan torsi pada pusat rotasi dinyatakan oleh: Στ = I x α (F x (2R - h)) - (w x d) = I x α. Dengan hubungan trigonometri pada segitiga siku-siku di titik poros rotasi, diperoleh: R² = (R-h)² + d² R² = R² - 2Rh + h² + d² d² = 2Rh - h² d = √( 2Rh - h² ) d = √( 2xRx(R/5) - (R/5)² ) d = √( 2/5 R² - 1/25 R²) d = √(9/25 R²) d = 3/5 R. Maka, besar percepatan sudut sesaat pusat massa silinder adalah: (F x (2R - h)) - (w x d) = I x α (F x (2R - [R/5])) - (m x g x 3/5 x R) = 1/2 x m x R² x α (F x 9/5 R) - (3/5 mgR) = 1/2 x m x R² x α ----> kalikan dengan 10/R 18F - 6mg = 5mRα α = 3 (6F - 2mg) / (5mR). Oleh karena itu, jawaban yang benar adalah 3 (6F - 2mg) / (5mR), tidak ada pilihan yang sesuai.