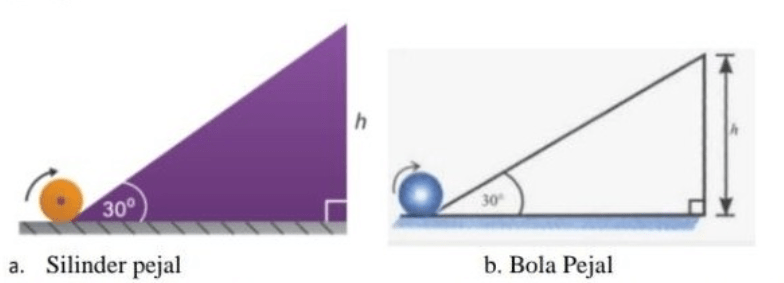
Sebuah silinder pejal dan bola pejal menggelinding menaiki suatu bidang miring seperti pada gambar berikut. Dua buah benda memiliki massa yang sama, masing – masing berbentuk bola pejal (I = 2/5 m.R^2) dan silinder berongga ( I = m.R^2). Keduanya bergerak menggelinding tanpa tergelincir mendaki bidang miring kasar yang sama dengan kecepatan yang sama sebesar 5 m/s. Bidang miring ini memiliki sudut kemiringan elevasi α dengan sin α = 0,5. Jika percepatan grafitasi g = 10 m/s^2 dan kedua benda mencapai tinggi maksimum. Tentukan tinggi maksimum yang dicapai bola pejal dan silinder berongga !

<p>Jawaban : 1,75 m dan 2,5 m</p><p>&nbsp;</p><p>Diketahui :</p><p>v1b = v1s = 5 m/s</p><p>h1b = h2b = 0 m</p><p>v2b = v2s = 0 m/s</p><p>&nbsp;</p><p>Ditanya :</p><p>h2b dan h2s ?</p><p>&nbsp;</p><p>Pembahasan :</p><p>Kekekalan energi mekanik merupakan suatu energi mekanik yang bernilai sama di setiap kondisi.</p><p>&nbsp;</p><p>Em1 = Em2</p><p>Ek1 + Ep1 = Ek2 + Ep2</p><p>&nbsp;</p><p>dengan&nbsp;</p><p>Em = energi mekanik (J)</p><p>Ek = energi kinetik (J)</p><p>Ep = energi potensial (J)</p><p>&nbsp;</p><p>1. Menghitung tinggi maksimum bola pejal</p><p>Ek1b + Ep1b = Ek2b + Ep2b</p><p>1/2 x mb x v1b² + 1/2 x Ib x ω² + 0 = 0 + mb x g x h2b</p><p>1/2 x mb x v1b² + 1/2 x 2/5 x mb x R² x v1b²/R² = mb x g x h2b</p><p>1/2 x 5² + 1/5 x 5²= 10 x h2b</p><p>7/10 x 25 = 10 x h2b</p><p>h2b = 7/4</p><p>h2b = 1,75 m&nbsp;</p><p>&nbsp;</p><p>2. Menghitung tinggi maksimum silinder berongga</p><p>Ek1s + Ep1s = Ek2s + Ep2s</p><p>1/2 x ms x v1s² + 1/2 x Is x ω² + 0 = 0 + ms x g x h2s</p><p>1/2 x ms x v1s² + 1/2 x &nbsp;ms x R² x v1s²/R² = ms x g x h2s</p><p>1/2 x 5² + 1/2 x 5²= 10 x h2s</p><p>25 = 10 x h2s</p><p>h2s = 2,5 m&nbsp;</p><p>&nbsp;</p><p>Dengan demikian, tinggi maksimum bola pejal dan silinder berongga adalah 1,75 m dan 2,5 m.</p>