Laila A
25 Juli 2024 07:23
Iklan
Laila A
25 Juli 2024 07:23
Pertanyaan
Sebuah persegi ABCD secara berturut turut terletak pada titik A(1, 1) B(4, 1) C(4,4) dan D(1, 4) Tentukanlah persamaan lingkaran yang menyinggung keempat sisi persegi ABCD tersebut!
Sebuah persegi ABCD secara berturut turut terletak pada titik A(1, 1) B(4, 1) C(4,4) dan D(1, 4) Tentukanlah persamaan lingkaran yang menyinggung keempat sisi persegi ABCD tersebut!


Belajar bareng Champions
Brain Academy Champions
Hanya di Brain Academy
Habis dalam
00
:
05
:
02
:
38
330
2
Iklan
Tiara S
25 Juli 2024 07:52
<p>Untuk menentukan persamaan lingkaran yang menyinggung keempat sisi persegi ABCD dengan titik-titik A(1, 1), B(4, 1), C(4, 4), dan D(1, 4), kita perlu mencari pusat dan jari-jari lingkaran tersebut.</p><p>Pusat persegi adalah titik tengah diagonal-diagonalnya. Titik tengah diagonal-diagonal persegi ABCD dapat dihitung sebagai berikut:</p><p> </p><p>Pusat = ( (xA+ xC)/2, (yA + yC)/2 )</p><p> = ( (1 + 4)/2, (1 + 4)/2 ) </p><p> = (2,5 , 2,5)</p><p> </p><p>Karena lingkaran tersebut menyinggung keempat sisi persegi, maka jari-jari lingkaran adalah setengah dari panjang sisi persegi. Panjang sisi persegi dapat dihitung sebagai jarak antara dua titik berurutan, misalnya A dan B:</p><p> </p><p>Panjang sisi = |xB - xA| = |4 - 1| = 3</p><p> </p><p>Jadi, jari-jari lingkaran adalah setengah dari panjang sisi:</p><p> </p><p>Jari-jari = 3/2 = 1,5 </p><p> </p><p>Dengan pusat di (2,5 , 2,5) dan jari-jari 1,5, persamaan lingkaran dapat dituliskan sebagai:</p><p> </p><p>(x - 2,5)<sup>2 </sup>+ (y - 2,5)<sup>2 </sup>= 1,5<sup>2</sup></p><p> </p><p>Menyederhanakan jari-jari:</p><p> </p><p>1,5<sup>2 </sup>= 2,25</p><p> </p><p>Jadi, persamaan lingkarannya adalah:</p><p> </p><p>(x - 2,5)<sup>2 </sup>+ (y - 2,5)<sup>2</sup>= 2,25</p>
Untuk menentukan persamaan lingkaran yang menyinggung keempat sisi persegi ABCD dengan titik-titik A(1, 1), B(4, 1), C(4, 4), dan D(1, 4), kita perlu mencari pusat dan jari-jari lingkaran tersebut.
Pusat persegi adalah titik tengah diagonal-diagonalnya. Titik tengah diagonal-diagonal persegi ABCD dapat dihitung sebagai berikut:
Pusat = ( (xA+ xC)/2, (yA + yC)/2 )
= ( (1 + 4)/2, (1 + 4)/2 )
= (2,5 , 2,5)
Karena lingkaran tersebut menyinggung keempat sisi persegi, maka jari-jari lingkaran adalah setengah dari panjang sisi persegi. Panjang sisi persegi dapat dihitung sebagai jarak antara dua titik berurutan, misalnya A dan B:
Panjang sisi = |xB - xA| = |4 - 1| = 3
Jadi, jari-jari lingkaran adalah setengah dari panjang sisi:
Jari-jari = 3/2 = 1,5
Dengan pusat di (2,5 , 2,5) dan jari-jari 1,5, persamaan lingkaran dapat dituliskan sebagai:
(x - 2,5)2 + (y - 2,5)2 = 1,52
Menyederhanakan jari-jari:
1,52 = 2,25
Jadi, persamaan lingkarannya adalah:
(x - 2,5)2 + (y - 2,5)2= 2,25
· 5.0 (2)
Iklan
Samudra A

Community
25 Juli 2024 10:00
<p>Semoga paham</p>
Semoga paham
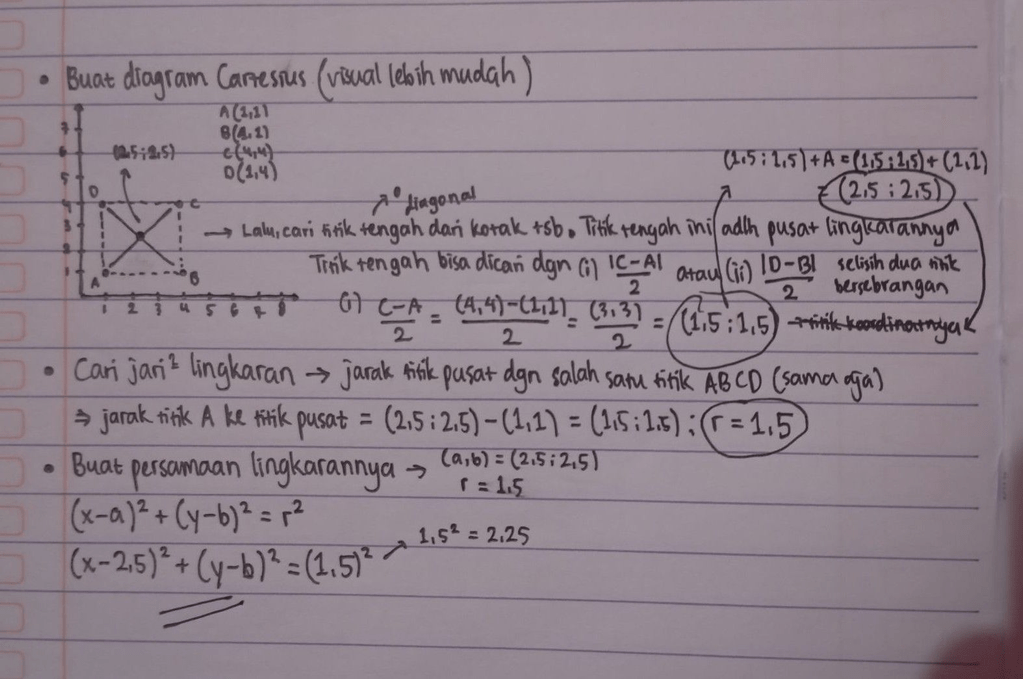
· 0.0 (0)
Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
Iklan

