Winda S
19 Agustus 2022 23:42
Iklan
Winda S
19 Agustus 2022 23:42
Pertanyaan
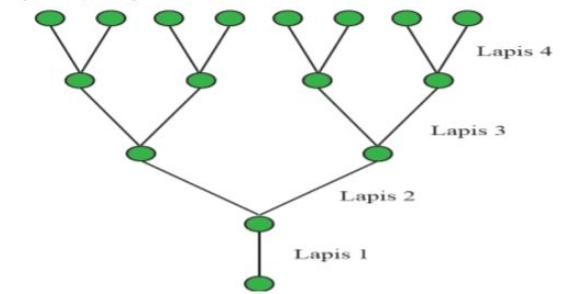
Sebuah cabang pohon terus bercabang dengan pola teratur seperti ditunjukkan pada gambar berikut Tentukan jumlah cabang pada lapis ke: 101( nyatakan dalam bentuk bilangan berpangkat )
1
1
Iklan
C. Salsa
Mahasiswa/Alumni Universitas Gajah Mada
03 Desember 2022 10:42
<p>Jawaban : 2^(100) </p><p> </p><p>Ingat! </p><p>Suku ke-n pada barisan geometri adalah Un = ar^(n-1) </p><p>dengan a : suku pertama </p><p>r : rasio </p><p>r = Un/U(n-1) </p><p> </p><p>Lapis 1 : 1 </p><p>Lapis 2 : 2 </p><p>Lapis 3 : 4 </p><p>Lapis 4 : 8 </p><p> </p><p>Sehingga terbentuk barisan bilangan: 1, 2, 4, 8</p><p> </p><p>Diperoleh a = 1 </p><p>r = 2/1 = 2 </p><p> </p><p>Sehingga </p><p>Un = 1•2^(n-1) </p><p>Un = 2^(n-1) </p><p> </p><p>Untuk n = 101, maka </p><p>U101 = 2^(101-1) = 2^(100) </p><p> </p><p>Jadi, jumlah cabang pada lapis ke-101 adalah 2^(100)</p>
Jawaban : 2^(100)
Ingat!
Suku ke-n pada barisan geometri adalah Un = ar^(n-1)
dengan a : suku pertama
r : rasio
r = Un/U(n-1)
Lapis 1 : 1
Lapis 2 : 2
Lapis 3 : 4
Lapis 4 : 8
Sehingga terbentuk barisan bilangan: 1, 2, 4, 8
Diperoleh a = 1
r = 2/1 = 2
Sehingga
Un = 1•2^(n-1)
Un = 2^(n-1)
Untuk n = 101, maka
U101 = 2^(101-1) = 2^(100)
Jadi, jumlah cabang pada lapis ke-101 adalah 2^(100)
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu
LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian
Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
