Angga R
01 Juli 2022 08:15
Iklan
Angga R
01 Juli 2022 08:15
Pertanyaan
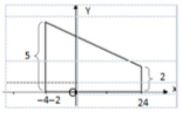
Sebuah bidang berbentuk trapesium diletakkan dalam koordinat seperti gambar di bawah ini. Titik berat bidang di atas terhadap titik pusat koordinat O adalah .... A. (4/7, 13/7) B. (4/7, 8/7) C. (8/7, 10/7) D. (8/7, 13/7) E. (10/7, 13/7)
2
1
Iklan
S. SheilaTeacherAssisstant
Mahasiswa/Alumni Universitas Pancasila
26 Oktober 2022 06:41
<p><strong>Jawaban: (8, 13/7) tidak ada di opsi.</strong></p><p> </p><p>Ingat!</p><p><strong>Titik berat benda suatu bidang datar:</strong></p><p><strong>x₀ = (x₁A₁ + x₂A₂ + x₃A₃ + … + x<sub>n</sub>A<sub>n</sub>)/(A₁ + A₂ + A₃ + … + A<sub>n</sub>)</strong></p><p><strong>y₀ = (y₁A₁ + y₂A₂ + y₃A₃ + … + y<sub>n</sub>A<sub>n</sub>)/(A₁ + A₂ + A₃ + … + A<sub>n</sub>)</strong></p><p><strong> </strong></p><p>Sementara titik berat beberapa bidang datar yang diketahui adalah:</p><p><strong>Persegi panjang:</strong></p><p><strong>A = p · ℓ</strong></p><p><strong>(x₀, y₀) = (½p, ½ℓ)</strong></p><p><strong>Segitiga:</strong></p><p><strong>A = ½ a · t</strong></p><p><strong>(x₀, y₀) = (⅓a, ⅓t) </strong></p><p>Dimana:</p><p>p = panjang persegi panjang</p><p>ℓ = lebar persegi panjang</p><p>a = alas segitiga</p><p>t = tinggi segitiga</p><p> </p><p>Dik:</p><p>Benda homogen berupa trapesium (gabungan persegi panjang dan segitiga siku-siku) seperti pada gambar.</p><p>Benda 1 : Persegi Panjang</p><p>Benda 2 : Segitiga</p><p>Dit: Z (titik berat)</p><p>Jawab:</p><p>Lihat gambar,</p><p>Benda 1:</p><p>p = 24 + 4 = 28</p><p>ℓ = 2</p><p>A₁ = p · ℓ</p><p>A₁ = 28 · 2</p><p><strong>A₁ = 56</strong></p><p>Titik berat dari O:</p><p>x₁ = 24 – ½p</p><p>x₁ = 24 – ½(28)</p><p>x₁ = 24 – 14</p><p><strong>x₁ = 10</strong></p><p>y₁ = ½ℓ</p><p>y₁ = ½ · 2</p><p><strong>y₁ = 1</strong></p><p> </p><p>Benda 2:</p><p>a = 24 + 4 = 28</p><p>t = 5 – 2 = 3</p><p>A₂ = ½ a · t</p><p>A₂ = ½ · 28 · 3</p><p><strong>A₂ = 42</strong></p><p>Titik berat dari O:</p><p>x₂ = ⅓a – 4</p><p>x₂ = ⅓ · 28 – 4</p><p>x₂ = 28/3 – 12/3</p><p><strong>x₂ = 16/3</strong></p><p>y₂ = 2 + ⅓t</p><p>y₂ = 2 + ⅓ · 3</p><p>y₂ = 2 + 1</p><p><strong>y₂ = 3</strong></p><p> </p><p>Maka, titik berat benda:</p><p>x₀ = (x₁A₁ + x₂A₂)/(A₁ + A₂)</p><p>x₀ = (10 · 56 + 16/3 · 42)/(56 + 42)</p><p>x₀ = (560 + 224)/98</p><p>x₀ = 784/98</p><p><strong>x₀ = 8</strong></p><p> </p><p>y₀ = (y₁A₁ + y₂A₂)/(A₁ + A₂)</p><p>y₀ = (1 · 56 + 3 · 42)/(56 + 42)</p><p>y₀ = (56 + 126)/98</p><p>y₀ = 182/98</p><p><strong>y₀ = 13/7</strong></p><p><strong>Titik berat benda (x₀, y₀) = (8, 13/7)</strong></p><p> </p><p><strong><u>Dengan demikian, titik berat bidang di atas terhadap titik pusat koordinat O adalah (8, 13/7) (tidak ada di opsi).</u></strong></p>
Jawaban: (8, 13/7) tidak ada di opsi.
Ingat!
Titik berat benda suatu bidang datar:
x₀ = (x₁A₁ + x₂A₂ + x₃A₃ + … + xnAn)/(A₁ + A₂ + A₃ + … + An)
y₀ = (y₁A₁ + y₂A₂ + y₃A₃ + … + ynAn)/(A₁ + A₂ + A₃ + … + An)
Sementara titik berat beberapa bidang datar yang diketahui adalah:
Persegi panjang:
A = p · ℓ
(x₀, y₀) = (½p, ½ℓ)
Segitiga:
A = ½ a · t
(x₀, y₀) = (⅓a, ⅓t)
Dimana:
p = panjang persegi panjang
ℓ = lebar persegi panjang
a = alas segitiga
t = tinggi segitiga
Dik:
Benda homogen berupa trapesium (gabungan persegi panjang dan segitiga siku-siku) seperti pada gambar.
Benda 1 : Persegi Panjang
Benda 2 : Segitiga
Dit: Z (titik berat)
Jawab:
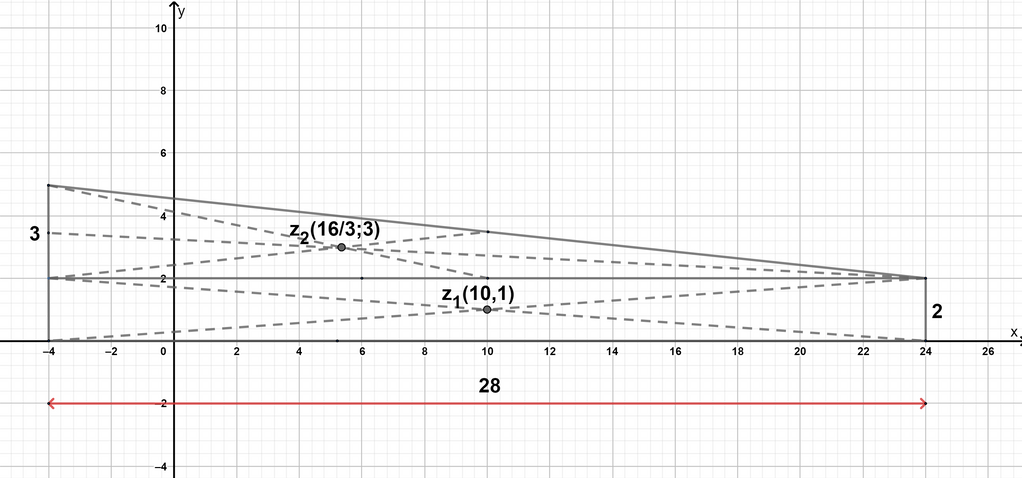
Lihat gambar,
Benda 1:
p = 24 + 4 = 28
ℓ = 2
A₁ = p · ℓ
A₁ = 28 · 2
A₁ = 56
Titik berat dari O:
x₁ = 24 – ½p
x₁ = 24 – ½(28)
x₁ = 24 – 14
x₁ = 10
y₁ = ½ℓ
y₁ = ½ · 2
y₁ = 1
Benda 2:
a = 24 + 4 = 28
t = 5 – 2 = 3
A₂ = ½ a · t
A₂ = ½ · 28 · 3
A₂ = 42
Titik berat dari O:
x₂ = ⅓a – 4
x₂ = ⅓ · 28 – 4
x₂ = 28/3 – 12/3
x₂ = 16/3
y₂ = 2 + ⅓t
y₂ = 2 + ⅓ · 3
y₂ = 2 + 1
y₂ = 3
Maka, titik berat benda:
x₀ = (x₁A₁ + x₂A₂)/(A₁ + A₂)
x₀ = (10 · 56 + 16/3 · 42)/(56 + 42)
x₀ = (560 + 224)/98
x₀ = 784/98
x₀ = 8
y₀ = (y₁A₁ + y₂A₂)/(A₁ + A₂)
y₀ = (1 · 56 + 3 · 42)/(56 + 42)
y₀ = (56 + 126)/98
y₀ = 182/98
y₀ = 13/7
Titik berat benda (x₀, y₀) = (8, 13/7)
Dengan demikian, titik berat bidang di atas terhadap titik pusat koordinat O adalah (8, 13/7) (tidak ada di opsi).
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



