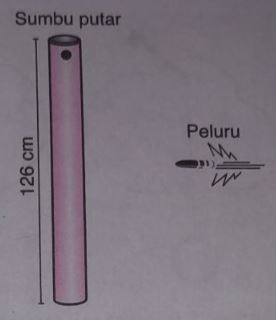
Sebuah batang berbentuk silinder bermassa 660 g dan memiliki panjang 126 cm. Batang tersebut digantungkan pada sumbu putar seperti tampak pada gambar di samping. Pada batang tersebut ditembakkan sebuah peluru yang bermassa 20 g secara mendatar. Kelajuan minimum peluru yang diperlukan agar peluru bersarang tepat di pusat batang dan batang dapat berputar satu putaran penuh adalah .... (g = 10 m/s²) a. 102 m/s b. 153 m/s c. 204 m/s d. 255 m/s e. 306 m/s

Question

Jawaban yang benar untuk pertanyaan tersebut adalah 196,335 m/s. Tidak ada opsi pilihan yang tepat.

Konsep yang digunakan dalam menjawab soal ini adalah hukum kekelan energi mekanik dan hukum kekekalan momentum sudut.akan digunakan untuk menyelesaikan persoalan tersebut.

Diketahui:
massa batang silinder (mb) = 660 gr = 0,66 kg
panjang batang silinder (lb) = 126 cm = 1,26 m
massa peluru (mp) = 20 gr =0,02 kg
panjang peluru bersarang dari sumbu (lp) = 63 cm = 0,63 m
percepatan gravitasi (g) = 10 m/s^2
I balok dengan sumbu di ujung = 1/3 x mb xlb^2
ω = v/r

Ditanya:

Kelajuan minimum ...?

Jawab:

Adapun langkah menyelesaikan soal ini:

1. Gunakan persamaan hukum kekekalan energi mekanik dimana energi mekanik:
Energi mekanik (EM) = E potensial gravitasi (Ep) + Energi kinetik (Ek) (rotasi dan translasi)
EM = m x g xh + 1/2 x m x V^2 + 1/2 x I x ω^2
Dengan:
m = massa (kg)
g = percepatan gravitasi (m/s^2)
v = kecepatan (m/s)
I = momen inersia (kgm^2)
ω = kecepatan sudut (rad/s)

Sehingga, hukum kekekalan energi mekanik:
EM1 = EM2
EM1 adalah energi mekanik awal pada saat batang silinder berada di bawah, dengan energi potensial relatif terhadap pusat batang adalah 0
EM2 adalah energi mekanik akhir saat batang silinder berada diatas (membentuk sudut 180 dari posisi awal), memiliki energi potensial relatif sebesar 2 kali lp
V1 = kecepatan setelah peluru bersarang
Sehingga:
EM1 = EM2
Ep 1 + Ek1 = Ep2 + Ek2
0 +( 1/2 x mp x V1^2 )+ (1/2 x I x ω^2) = (mp + mb) x g x h + 0
(1/2 x 0,02 x v1^2) +( 1/2 x 1/3 x 0,66 x 1,26 ^2 x (v1/lp)^2 )= (0,66 + 0,02) x 10 x 2 x lp
(0,01 x v1^2 )+ (0,11 x 1,26^2 x v1^2/0,63^2 ) = 0,68 x 10 x 1,26
(0,01 v1^2 )+ (0,11 x 4v1^2) = 8,568
0,45 V1^2 = 8,568
V1^2 = 19,04
V1 = 4,363 m/s

2. V1 adalah kecepatan peluru tepat di pusat batang sedangkan untuk kecepatan peluru sebelum bertumbukan dengan batang menggunakan hukum kekekalan momentum sudut
momentum sudut (L) = I x ω
Dengan vp' = v1 sehingga:
Lb + Lp = Lb' + Lp'
(I x ω ) + (mp x vp x lp) = (I x ω) + (mp x vp'x lp)
0 + (0,02 x vp x 0,63) = (1/3 x mb x lb^2 x (v1/lp)) +( 0,02 x v1 x 0,63)
0,0126 vp = (1/3 x 0,66 x 1,26^2 x (v1/0,63)) +( 0,0126 x v1)
0,0126 vp = 0,5544 x v1 + 0,0126 v1
0,0126 vp = 0,5544 x 4,363 + 0,0126 x 4,363
vp = 196,335 m/s

Jadi kecepatan peluru ditembakkan adalah 196,335 m/s. Tidak ada opsi pilihan yang tepat.

Mau pemahaman lebih dalam untuk soal ini?