Indra I
31 Juli 2022 08:54
Iklan
Indra I
31 Juli 2022 08:54
Pertanyaan
Rifqi menjual 2 jenis kaos kaki panjang dan pendek dengan modal Rp. 200.000. Harga beli kaos kaki panjang Rp.8.000/ pasang, dan harga beli kaos kaki pendek Rp. 4.000/pasang. Keuntungan yang diperoleh dari penjualan kaos kaki panjang Rp.7.000/pasang dan kaos kaki pendek Rp. 6000/pasang. Banyak kaos kaki yang dijual tidak lebih dari 35 pasang. Sedangkan kaos kaki pendek yang dibeli oleh rafqi tidak lebih dari 20 pasang. Jadi berapa keuntungan maksimal dan keuntungan minimal yang diperoleh oleh Rifqi?
17
1
Iklan
D. Nuryani
Mahasiswa/Alumni Universitas Padjadjaran
30 Oktober 2022 13:25
<p>Jawaban : keuntungan maksimal Rp225.000,00 dan keuntungan minimal Rp0,00.</p><p> </p><p>Langkah-langkah mencari daerah penyelesaian SPtLDV:<br>1) Gambar masing-masing grafik<br>2) Uji titik untuk mencari daerah pertidaksamaan<br>3) Cari daerah yang beririsan dari kedua pertidaksamaan</p><p> </p><p>Kemudian untuk mencari nilai optimum dari daerah penyelesaian dapat digunakan metode titik pojok (menyubstitusikan titik pojok pada fungsi objektif).</p><p> </p><p>Misalkan</p><p>x: kasos kaki panjang</p><p>y: kasos kaki pendek</p><p> </p><p>Model SPtLDV</p><p>8.000x + 4.000y <= 200.000</p><p>______________________:4.000</p><p>2x + y <= 50 </p><p>x + y <= 35 </p><p>y <= 20</p><p> </p><p>Fungsi objektif f(x,y) = 7.000x + 6.000y</p><p> </p><p>Pertama, gambarkan grafiknya<br>Grafik 2x + y = 50 <br>▪️ Titik potong sumbu X, y = 0<br>2x + y = 50 </p><p>2x + 0 = 50</p><p>2x = 50</p><p>x = 25</p><p>(25, 0)<br>▪️ Titik potong sumbu Y, x = 0<br>2x + y = 50 </p><p>2(0) + y = 50</p><p>y = 50</p><p>(0, 50)</p><p> </p><p>Uji daerah pada titik (0, 0)<br>2x + y ... 50 <br>0+0 ... 50<br>0 < 50<br>sehingga daerah penyelesaian 2x + y <= 50 melewati titik (0,0)</p><p> </p><p>Grafik x + y = 35 <br>▪️ Titik potong sumbu X, y = 0<br>x + y = 35 </p><p>x + 0 = 35</p><p>x = 35</p><p>(35, 0)<br>▪️ Titik potong sumbu Y, x = 0<br>x + y = 35 </p><p>0 + y = 35</p><p>y = 35</p><p>(0, 35)</p><p> </p><p>Uji daerah pada titik (0, 0)<br>x + y ... 35 <br>0+0 ... 35<br>0 < 35<br>sehingga daerah penyelesaian x + y <= 35 melewati titik (0,0)</p><p> </p><p>x ≥ 0 ----> daerah penyelesaian berada di sebelah kanan sumbu Y<br>y ≥ 0 ----> daerah penyelesaian berada di atas sumbu X</p><p> </p><p>Cari titik potong kedua garis</p><p>2x + y = 50</p><p>x + y = 35</p><p>_________-</p><p>x = 15</p><p> </p><p>x + y = 35</p><p>15 + y = 35</p><p>y = 35 - 15</p><p>y = 20</p><p>(15, 20)</p><p> </p><p>Gambarkan daerah penyelesaian pada bidang kartesius (dilampirkan)</p><p> </p><p>Diperoleh berdasarkan gambar bahwa titik pojoknya adalah</p><p>(0,0) ---> 7.000(0) + 6.000(0) = 0 (min)</p><p>(0,35) ----> 7.000(0) + 6.000(35) = 210.000</p><p>(15,20) ----> 7.000(15) + 6.000(20) = 225.000 (maks)</p><p>(25,0) ---> 7.000(25) + 6.000(0) = 175.000</p><p> </p><p>Jadi, keuntungan maksimal Rp225.000,00 dan keuntungan minimal Rp0,00.</p>
Jawaban : keuntungan maksimal Rp225.000,00 dan keuntungan minimal Rp0,00.
Langkah-langkah mencari daerah penyelesaian SPtLDV:
1) Gambar masing-masing grafik
2) Uji titik untuk mencari daerah pertidaksamaan
3) Cari daerah yang beririsan dari kedua pertidaksamaan
Kemudian untuk mencari nilai optimum dari daerah penyelesaian dapat digunakan metode titik pojok (menyubstitusikan titik pojok pada fungsi objektif).
Misalkan
x: kasos kaki panjang
y: kasos kaki pendek
Model SPtLDV
8.000x + 4.000y <= 200.000
______________________:4.000
2x + y <= 50
x + y <= 35
y <= 20
Fungsi objektif f(x,y) = 7.000x + 6.000y
Pertama, gambarkan grafiknya
Grafik 2x + y = 50
▪️ Titik potong sumbu X, y = 0
2x + y = 50
2x + 0 = 50
2x = 50
x = 25
(25, 0)
▪️ Titik potong sumbu Y, x = 0
2x + y = 50
2(0) + y = 50
y = 50
(0, 50)
Uji daerah pada titik (0, 0)
2x + y ... 50
0+0 ... 50
0 < 50
sehingga daerah penyelesaian 2x + y <= 50 melewati titik (0,0)
Grafik x + y = 35
▪️ Titik potong sumbu X, y = 0
x + y = 35
x + 0 = 35
x = 35
(35, 0)
▪️ Titik potong sumbu Y, x = 0
x + y = 35
0 + y = 35
y = 35
(0, 35)
Uji daerah pada titik (0, 0)
x + y ... 35
0+0 ... 35
0 < 35
sehingga daerah penyelesaian x + y <= 35 melewati titik (0,0)
x ≥ 0 ----> daerah penyelesaian berada di sebelah kanan sumbu Y
y ≥ 0 ----> daerah penyelesaian berada di atas sumbu X
Cari titik potong kedua garis
2x + y = 50
x + y = 35
_________-
x = 15
x + y = 35
15 + y = 35
y = 35 - 15
y = 20
(15, 20)
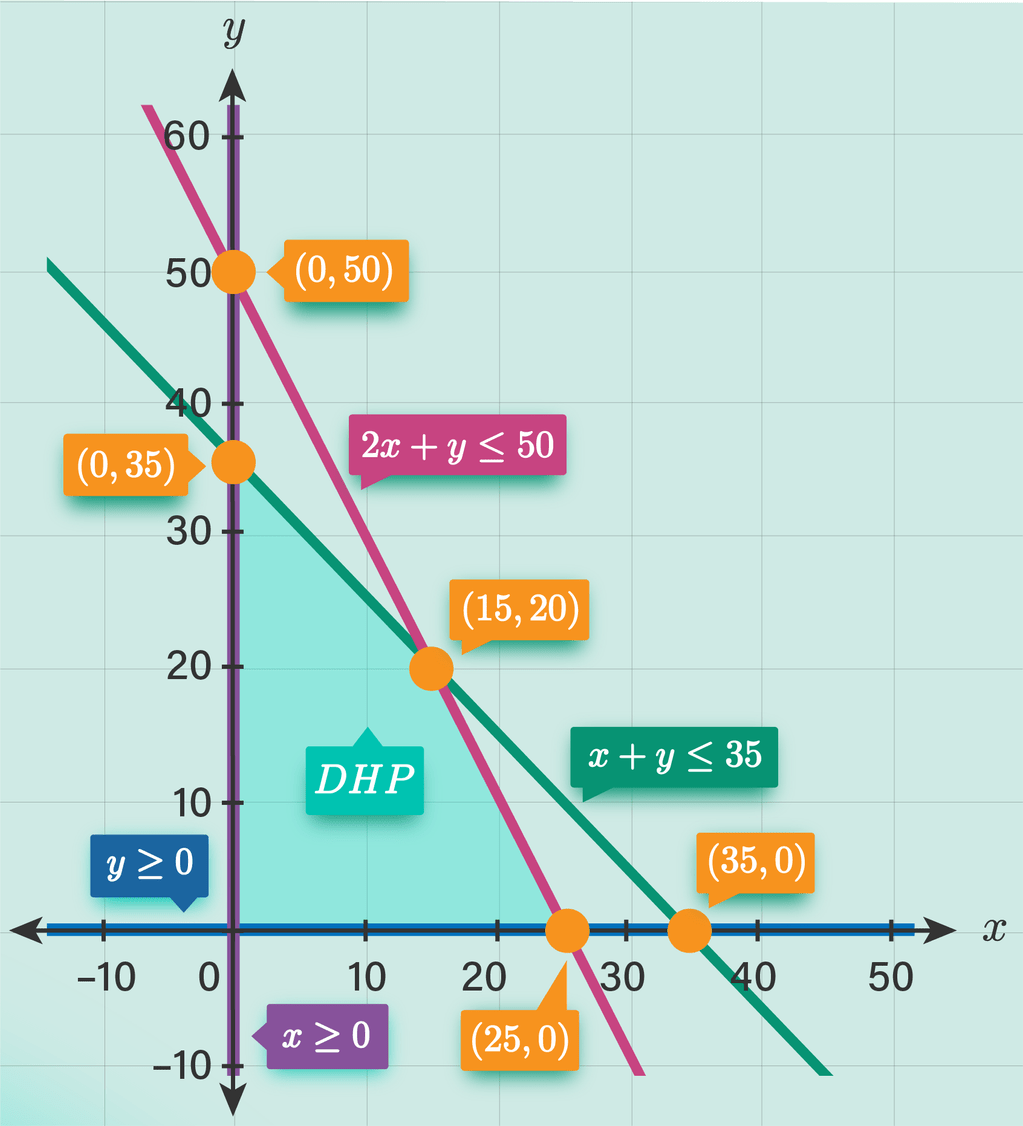
Gambarkan daerah penyelesaian pada bidang kartesius (dilampirkan)
Diperoleh berdasarkan gambar bahwa titik pojoknya adalah
(0,0) ---> 7.000(0) + 6.000(0) = 0 (min)
(0,35) ----> 7.000(0) + 6.000(35) = 210.000
(15,20) ----> 7.000(15) + 6.000(20) = 225.000 (maks)
(25,0) ---> 7.000(25) + 6.000(0) = 175.000
Jadi, keuntungan maksimal Rp225.000,00 dan keuntungan minimal Rp0,00.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



