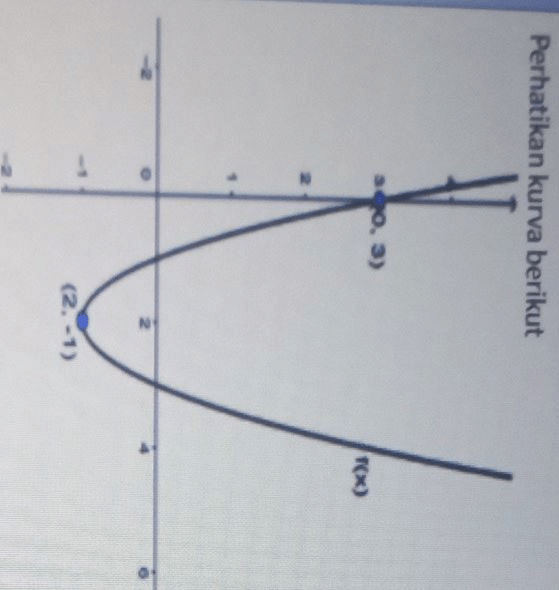
Perhatikan kurva berikut. Jika kurva parabola pada gambar tersebut di rotasi 25° dilanjutkan 65° searah jarum jam dengan pusat (0,0) maka persamaan kurva hasil rotasi tersebut adalah .... A. y = x² − 4x + 3 B. y = x² + 4x + 3 C. x = y² − 4y + 3 D. x = y² + 4y + 3 E. x = −y² + 4y − 3

Question

Jawaban : x = y² + 4y + 3

Diketahui :

𝞱₁ = 25° dan 𝞱₂ = 65° dengan rotasi searah jarum jam, dan sebuah kurva parabola yang melalui titik puncak (x_p, y_p) = (2, -1) dan sembarang titik (0,3) seperti gambar di atas.

Ditanya :

persamaan bayangan dengan rotasi 𝞱₁ = 25° dan 𝞱₂ = 65° searah jarum jam

Jawab :

Persamaan parabola dengan titik puncak (x_p, y_p) adalah

y = a (x - x_p)² + y_p

Pada gambar di atas, kurva parabola melalui titik (x_p, y_p) = (2, -1) dan (x,y) = (0,3), sehingga diperoleh.

y = a (x - x_p)² + y_p

3 = a (0 - 2)² + (-1)

3 = a (-2)² - 1

3 = 4a - 1 --> 4a = 4 --> a = 1

Persamaan kuadrat kurva parabola adalah

y = (1) (x - 2)² - 1

y = x² - 4x + 4 - 1

y = x² - 4x + 3

𝞱₃= sudut total rotasi searah jarum jam

𝞱₃ = 𝞱₁ + 𝞱₂

𝞱₃ = 25° + 65°

𝞱₃ = 90°

Rotasi 90° searah jarum jam = rotasi 270° berlawanan jarum jam

Jika titik (x, y) dirotasikan 90° searah jarum jam, maka bayangannya adalah titik (y, -x).

Jadi (x', y') = (y, -x), sehingga diperoleh :

x' = y --> y = x'

y' = -x --> x = -y'

Persamaan bayangannya adalah

y = x² - 4x + 3

x' = (-y')² - 4(-y') + 3

x' = (y')² + 4y' + 3

ubah x' menjadi x, dan y' menjadi y, diperoleh

x = y² + 4y + 3

Kesimpulan : x = y² + 4y + 3

Perhatikan kurva berikut. Jika kurva parabola pada gambar tersebut di rotasi 25° dilanjutkan 65° searah jarum jam dengan pusat (0,0) maka persamaan kurva hasil rotasi tersebut adalah .... A. y = x² − 4x + 3 B. y = x² + 4x + 3 C. x = y² − 4y + 3 D. x = y² + 4y + 3 E. x = −y² + 4y − 3

Mau pemahaman lebih dalam untuk soal ini?

Pertanyaan serupa