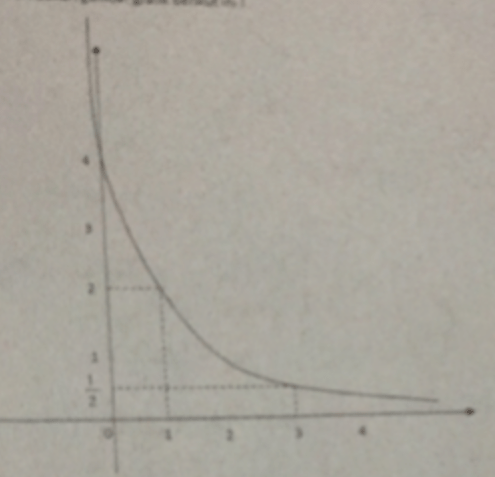
Perhatikan gambar grafik berikut! Tentukan rumus fungsi dari grafik tersebut!

Jawabannya adalah f(x) = ^(3^(-⅔)) log ((3^(-4/3))x) Ingat Bentuk umum persamaan logaritma jika diketahui 2 titik f(x) = ^a log (bx) Definisi logaritma ^a log b = c, maka b = a^c Dengan syarat a>0, a≠1 dan b>0 Fungsi eksponen (a^m) ^n = a^(mn) a^m / (a^n) = a^(m-n) 1/(a^m) = a^(-m) a^(m/n) = ⁿ√(a^m) Dari gambar diketahui 2titik yaitu (1,2) dan (3,½) Untuk titik (1,2) f(x) = ^a log (bx) 2 = ^a log (b(1)) 2 = ^a log b b = a² Untuk b =a² substitusikan ke f(x) = ^a log (bx) f(x) = ^a log (a²x) Substitusi titik kedua (3,½) f(x) = ^a log (a²x) ½ = ^a log (3a²) 3a² = a^(½) a² / (a^(½)) = ⅓ a^(2-½) = ⅓ a^(3/2) = 3^(-1) Kedua ruas dipangkatkan (2/3)menjadi (a^(3/2))^(2/3) = (3^(-1))^(2/3) a = 3^(-2/3) a = 1/(3^(⅔)) Sehingga persamaan logaritmanya menjadi f(x) = ^a log (a²x) f(x) = ^(1/(3^(⅔))) log ((1/(3^(⅔))²x) f(x) = ^(1/(3^(⅔))) log (1/3^(4/3))x) f(x) = ^(3^(-⅔)) log ((3^(-4/3))x) Jadi jawabnya rumus fungsi dari grafik diatas adalah f(x) = ^(3^(-⅔)) log ((3^(-4/3))x)