Almira D
25 Agustus 2022 01:01
Iklan
Almira D
25 Agustus 2022 01:01
Pertanyaan
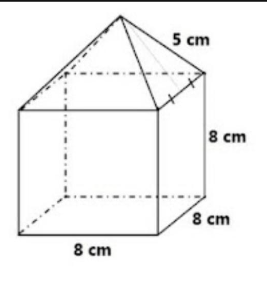
Perhatikan gambar berikut! Luas permukaan bangun ruang tersebut adalah.... A. 368 B. 468 C. 598 D. 698
2
1
Iklan
K. LATIPAH
Mahasiswa/Alumni ""
13 Desember 2022 08:01
<p>Jawabannya: A. 368 cm<sup>2</sup></p><p> </p><p>Ingat:</p><p>Luas permukaan (Lp) limas tanpa alas</p><p>Lp limas tanpa alas = jumlah luas sisi tegak</p><p> </p><p>Luas permukaan (Lp) kubus tanpa tutup</p><p>Lp. kubus tanpa tutup = 5 × r<sup>2</sup></p><p>dimana:</p><p>r = panjang rusuk kubus</p><p> </p><p>Luas gabungan = lp limas tanpa alas + lp. kubus tanpa tutup</p><p> </p><p>Teorema phytagoras</p><p>Kuadrat sisi miring sama dengan jumlah kuadrat sisi-sisi lainnya pada segitiga siku-siku. c adalah sisi miring, a dan b adalah sisi-sisi lainnya, maka</p><p>c<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup> </p><p> </p><p>Pada soal diketahui panjang rusuk kubus adalah 8 cm, Pertama kita cari luas permukaan kubus tanpa tutup.</p><p>Lp. Kubus tanpa tutup = 5 × r<sup>2</sup></p><p>Lp. Kubus tanpa tutup = 5 × 8<sup>2</sup></p><p>Lp. Kubus tanpa tutup = 5 × 64</p><p>Lp. Kubus tanpa tutup = 320 cm<sup>2</sup></p><p> </p><p>Misalkan tinggi segitiga pada limas adalah To dan O terletak ditengah-tengah FG, dimana panjang OF = OG = 1/2(8 cm) = 4 cm</p><p>maka</p><p>(TO)<sup>2</sup> = (TG)<sup>2</sup> - (FG)<sup>2</sup></p><p>(TO)<sup>2</sup> = (5)<sup>2</sup> - (4)<sup>2</sup></p><p>(TO)<sup>2</sup> = 25 - 16</p><p>(TO)<sup>2</sup> = 9</p><p>TO = ±√9</p><p>TO = ± 3 cm (ambil yang bernilai positif)</p><p>TO = 3cm</p><p>sehingga</p><p>Lp. limas tanpa alas = Jumlah luas sisi tegak</p><p>Lp. Limas tanpa alas = 4 (1/2)(alas × tinggi)</p><p>Lp. limas tanpa alas = 2(8×3)</p><p>Lp. limas tanpa alas = 48 cm<sup>2</sup></p><p> </p><p>Luas gabungan = lp limas tanpa alas + lp. kubus tanpa tutup</p><p>Luas gabungan = 48 cm<sup>2</sup> + 320 cm<sup>2</sup></p><p>Luas gabungan = 368 cm<sup>2</sup></p><p> </p><p>Jadi luas gabungan dari bangunan di atas adalah 368 cm<sup>2</sup>. Oleh karena itu jawaban yang benar adalah A. 368 cm<sup>2</sup>.</p><p> </p>
Jawabannya: A. 368 cm2
Ingat:
Luas permukaan (Lp) limas tanpa alas
Lp limas tanpa alas = jumlah luas sisi tegak
Luas permukaan (Lp) kubus tanpa tutup
Lp. kubus tanpa tutup = 5 × r2
dimana:
r = panjang rusuk kubus
Luas gabungan = lp limas tanpa alas + lp. kubus tanpa tutup
Teorema phytagoras
Kuadrat sisi miring sama dengan jumlah kuadrat sisi-sisi lainnya pada segitiga siku-siku. c adalah sisi miring, a dan b adalah sisi-sisi lainnya, maka
c2 = a2 + b2
Pada soal diketahui panjang rusuk kubus adalah 8 cm, Pertama kita cari luas permukaan kubus tanpa tutup.
Lp. Kubus tanpa tutup = 5 × r2
Lp. Kubus tanpa tutup = 5 × 82
Lp. Kubus tanpa tutup = 5 × 64
Lp. Kubus tanpa tutup = 320 cm2
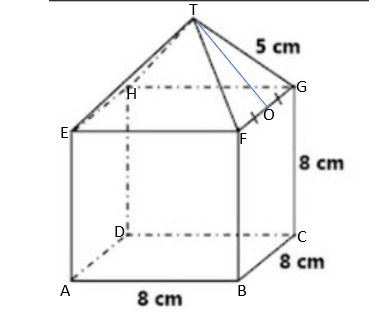
Misalkan tinggi segitiga pada limas adalah To dan O terletak ditengah-tengah FG, dimana panjang OF = OG = 1/2(8 cm) = 4 cm
maka
(TO)2 = (TG)2 - (FG)2
(TO)2 = (5)2 - (4)2
(TO)2 = 25 - 16
(TO)2 = 9
TO = ±√9
TO = ± 3 cm (ambil yang bernilai positif)
TO = 3cm
sehingga
Lp. limas tanpa alas = Jumlah luas sisi tegak
Lp. Limas tanpa alas = 4 (1/2)(alas × tinggi)
Lp. limas tanpa alas = 2(8×3)
Lp. limas tanpa alas = 48 cm2
Luas gabungan = lp limas tanpa alas + lp. kubus tanpa tutup
Luas gabungan = 48 cm2 + 320 cm2
Luas gabungan = 368 cm2
Jadi luas gabungan dari bangunan di atas adalah 368 cm2. Oleh karena itu jawaban yang benar adalah A. 368 cm2.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



