Putri M
14 Januari 2023 17:24
Iklan
Putri M
14 Januari 2023 17:24
Pertanyaan
Perhatikan gambar ! Berapakah luas bangun tersebut?
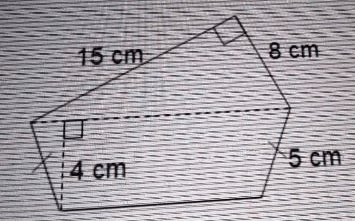
2
1
Iklan
A. Meylin
Mahasiswa/Alumni Universitas Airlangga
08 Februari 2023 01:06
<p>Jawaban yang benar adalah 116 cm<sup>2</sup>.</p><p> </p><p>Ingat rumus untuk menentukan luas (L) segitiga adalah:</p><p>L = 1/2 x alas x tinggi</p><p>Rumus untuk menentukan luas (L) trapesium adalah:</p><p>L = 1/2 x jumlah sisi sejajar x tinggi trapesium</p><p> </p><p>Pembahasan :</p><p>Perhatikan gambar dibawah!</p><p> </p><p>* Menentukan panjang AB dengan teorema pythagoras sebagai berikut:</p><p>AB<sup>2</sup> = AC<sup>2</sup> + BC<sup>2</sup></p><p>AB<sup>2</sup> = 15<sup>2</sup> + 8<sup>2</sup></p><p>AB<sup>2</sup> = 225 + 64</p><p>AB<sup>2</sup> = 289</p><p>AB = ±√(289)</p><p>AB = ±17 cm</p><p>karena panjang AB tidak mungkin negatif maka diperoleh panjang AB = 17 cm</p><p> </p><p>Luas segitiga ABC dengan alas = BC = 8 cm dan tinggi = AC = 15 cm adalah:</p><p>L.ABC = 1/2 x alas x tinggi</p><p>= 1/2 x 8 x 15</p><p>= 120/2</p><p>= 60 cm<sup>2</sup></p><p> </p><p>* Menentukan panjang AG dengan panjang AD = BE = 5 cm dan panjang DG = EF = 4 cm menggunakan teorema pythagoras sebagai berikut:</p><p>AG<sup>2</sup> = AD<sup>2</sup> - DG<sup>2</sup></p><p>AG<sup>2</sup> = 5<sup>2</sup> - 4<sup>2</sup></p><p>AG<sup>2</sup> = 25 - 16</p><p>AG<sup>2</sup> = 9</p><p>AG = ±√(9)</p><p>AG = ±3 cm</p><p>karena panjang AG tidak mungkin negatif maka diperoleh panjang AG = 3 cm.</p><p> </p><p>Panjang AG = FB = 3 cm, sehingga panjang DE = 17 - 3 - 3 = 11 cm.</p><p> </p><p>Luas trapesium ADEB dengan panjang sisi sejajar AB = 17 cm dan DE = 11 cm, tinggi trapesium = DG = 4 cm adalah:</p><p>L.ADEB = 1/2 x jumlah sisi sejajar x tinggi trapesium</p><p>= 1/2 x (17 + 11) x 4</p><p>= 1/2 x 28 x 4</p><p>= 112/2</p><p>= 56 cm<sup>2</sup></p><p> </p><p>maka luas bangun = L.ABC + L.ADEB = 60 + 56 = 116 cm<sup>2</sup>.</p><p> </p><p>Jadi, luas bangun tersebut adalah 116 cm<sup>2</sup>.</p><p>Semoga membantu ya.</p>
Jawaban yang benar adalah 116 cm2.
Ingat rumus untuk menentukan luas (L) segitiga adalah:
L = 1/2 x alas x tinggi
Rumus untuk menentukan luas (L) trapesium adalah:
L = 1/2 x jumlah sisi sejajar x tinggi trapesium
Pembahasan :
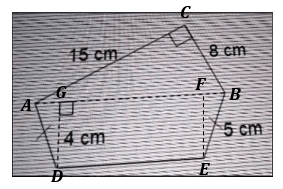
Perhatikan gambar dibawah!
* Menentukan panjang AB dengan teorema pythagoras sebagai berikut:
AB2 = AC2 + BC2
AB2 = 152 + 82
AB2 = 225 + 64
AB2 = 289
AB = ±√(289)
AB = ±17 cm
karena panjang AB tidak mungkin negatif maka diperoleh panjang AB = 17 cm
Luas segitiga ABC dengan alas = BC = 8 cm dan tinggi = AC = 15 cm adalah:
L.ABC = 1/2 x alas x tinggi
= 1/2 x 8 x 15
= 120/2
= 60 cm2
* Menentukan panjang AG dengan panjang AD = BE = 5 cm dan panjang DG = EF = 4 cm menggunakan teorema pythagoras sebagai berikut:
AG2 = AD2 - DG2
AG2 = 52 - 42
AG2 = 25 - 16
AG2 = 9
AG = ±√(9)
AG = ±3 cm
karena panjang AG tidak mungkin negatif maka diperoleh panjang AG = 3 cm.
Panjang AG = FB = 3 cm, sehingga panjang DE = 17 - 3 - 3 = 11 cm.
Luas trapesium ADEB dengan panjang sisi sejajar AB = 17 cm dan DE = 11 cm, tinggi trapesium = DG = 4 cm adalah:
L.ADEB = 1/2 x jumlah sisi sejajar x tinggi trapesium
= 1/2 x (17 + 11) x 4
= 1/2 x 28 x 4
= 112/2
= 56 cm2
maka luas bangun = L.ABC + L.ADEB = 60 + 56 = 116 cm2.
Jadi, luas bangun tersebut adalah 116 cm2.
Semoga membantu ya.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



