NAYLA N

16 Agustus 2023 15:24
Iklan
NAYLA N

16 Agustus 2023 15:24
Pertanyaan
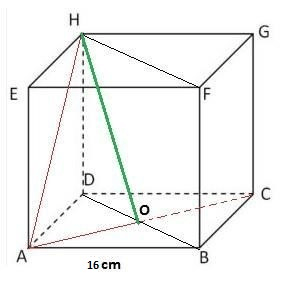
Panjang proyeksi garis AH terhadap bidang BDHF pada kubus ABCDEFGH yang memiliki panjang rusuk 16 cm adalah... cm A.8√6 B.8√3 C.8√2 D.4√6 E.4√3
Panjang proyeksi garis AH terhadap bidang BDHF pada kubus ABCDEFGH yang memiliki panjang rusuk 16 cm adalah... cm
A.8√6
B.8√3
C.8√2
D.4√6
E.4√3
24
2
Iklan
BimBim B
17 Agustus 2023 03:05
<h2>Jawabannya adalah A. 8√6.</h2><p> </p><p>Penjelasan</p><p><u>Diketahui</u></p><p>Kubus ABCD.EFGH dengan</p><ul><li>Panjang rusuk = 16 cm</li></ul><p> </p><p><u>Ditanyakan</u></p><p>Panjang proyeksi garis AH pada bidang BDHF = …. ?</p><p> </p><p><u>Jawab</u></p><p>Perhatikan kubus ABCD.EFGH pada lampiran</p><ul><li>H terletak pada pada BDHF</li><li>Tarik garis dari titik A ke C sehingga berpotongan dengan BD di titik O, sehingga AO tegak lurus dengan BDHF.</li></ul><p>Karena AO tegak lurus dengan BDHF, maka proyeksi AH pada bidang BDHF adalah HO</p><p> </p><p>Perhatikan segitiga AHO siku-siku di O, memiliki ukuran</p><ul><li>AH = 16√2 cm (AH adalah diagonal sisi)</li><li>AO = ½ AC = ½ (16√2 cm) = 8√2 (AC adalah diagonal sisi)</li></ul><p> </p><p>Jadi <strong>dengan menggunakan teorema Pythagoras</strong>, diperoleh:</p><p>HO = √(AH² – AO²)</p><p>HO = √((16√2)² – (8√2)²)</p><p>HO = √(512 – 128)</p><p>HO = √(384)</p><p>HO = √(64 . 6)</p><p><strong>HO = 8√6</strong></p><p> </p><p>Jadi <strong>panjang proyeksi AH pada bidang BDHF</strong> adalah <strong>HO = 8√6 cm</strong></p>
Jawabannya adalah A. 8√6.
Penjelasan
Diketahui
Kubus ABCD.EFGH dengan
- Panjang rusuk = 16 cm
Ditanyakan
Panjang proyeksi garis AH pada bidang BDHF = …. ?
Jawab
Perhatikan kubus ABCD.EFGH pada lampiran
- H terletak pada pada BDHF
- Tarik garis dari titik A ke C sehingga berpotongan dengan BD di titik O, sehingga AO tegak lurus dengan BDHF.
Karena AO tegak lurus dengan BDHF, maka proyeksi AH pada bidang BDHF adalah HO
Perhatikan segitiga AHO siku-siku di O, memiliki ukuran
- AH = 16√2 cm (AH adalah diagonal sisi)
- AO = ½ AC = ½ (16√2 cm) = 8√2 (AC adalah diagonal sisi)
Jadi dengan menggunakan teorema Pythagoras, diperoleh:
HO = √(AH² – AO²)
HO = √((16√2)² – (8√2)²)
HO = √(512 – 128)
HO = √(384)
HO = √(64 . 6)
HO = 8√6
Jadi panjang proyeksi AH pada bidang BDHF adalah HO = 8√6 cm
· 5.0 (5)
Iklan
Aveline A
16 Agustus 2023 18:43
Jawaban c
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



