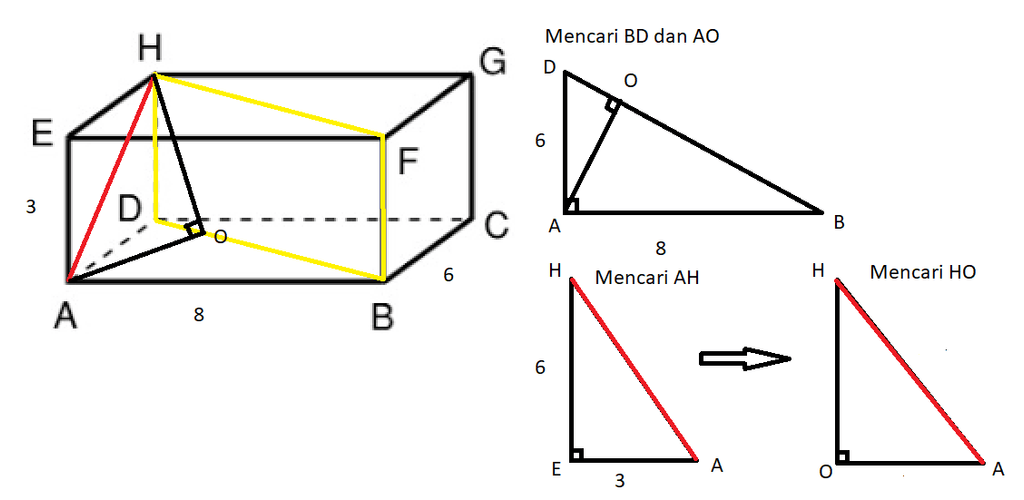
panjang proyeksi garis AH dengan bidang BDHF pada balok ABCD.EFGH yang panjang AB=8cm, BC=6 cm, dan AE=3cm adalah.....cm a. √73 b. 4 c. 3√5 d. √34 e. √109

<p>Jawaban : 3/5 √61 (tidak ada pada pilihan jawaban)</p><p>&nbsp;</p><p>Pembahasan :</p><p>Untuk memproyeksikan suatu titik atau sebuah garis pada suatu objek diperlukan satu garis yang akan memproyeksikan atau mencerminkan titik dan garis tersebut ke suatu objek yang dituju. Garis tersebut itulah yang dinamakan <strong>garis proyektor—</strong>antara garis proyektor dan garis hasil proyeksinya selalu berpotongan tegak lurus.</p><p>&nbsp;</p><p>perhatikan gambar balok ABCD.EFGH, untuk mencari panjang proyeksi garis AH ke bidang BDHF, maka terlebih dulu, menentukan proyeksi titik A dan H ke bidang BDHF.</p><p>1) titik H diproyeksikan ke bidang BDHF ada di titik H.</p><p>2) titik A di proyeksikan ke bidang BDHF ada di titik O.</p><p>maka panjang proyeksi AH ke bidang BDHF adalah panjang HO</p><p>&nbsp;</p><p>perhatikan segitiga ABD, siku-siku di A.</p><p>menentukan panjang BD dengan menggunakan konsep pitagoras.</p><p>BD = √AB² + AD²</p><p>BD = √8² + 6²</p><p>BD = 10</p><p>panjang AO bisa diperoleh dengan menggunakan aturan luas segitiga.</p><p>1/2 . AB. AD = 1/2 . BD. AO</p><p>1/2 . 8. 6 = 1/2 . 10. AO</p><p>AO = 24/5</p><p>&nbsp;</p><p>perhatikan segitiag AHE, siku-siku di E.</p><p>AH = √EH² + EA²</p><p>AH = √6² + 3²</p><p>AH = 3√5</p><p>&nbsp;</p><p>perhatikan segitiga AHO siku-siku di O.</p><p>HO = √AH² - AO²</p><p>HO = √(3√5)² - (24/5)²</p><p>HO = 3/5 √61</p><p>&nbsp;</p><p>Jadi jawaban yang tepat adalah 3/5 √61</p>