KM
Kerenhapukh M
02 April 2020 04:51
Iklan
KM
Kerenhapukh M
02 April 2020 04:51
Pertanyaan
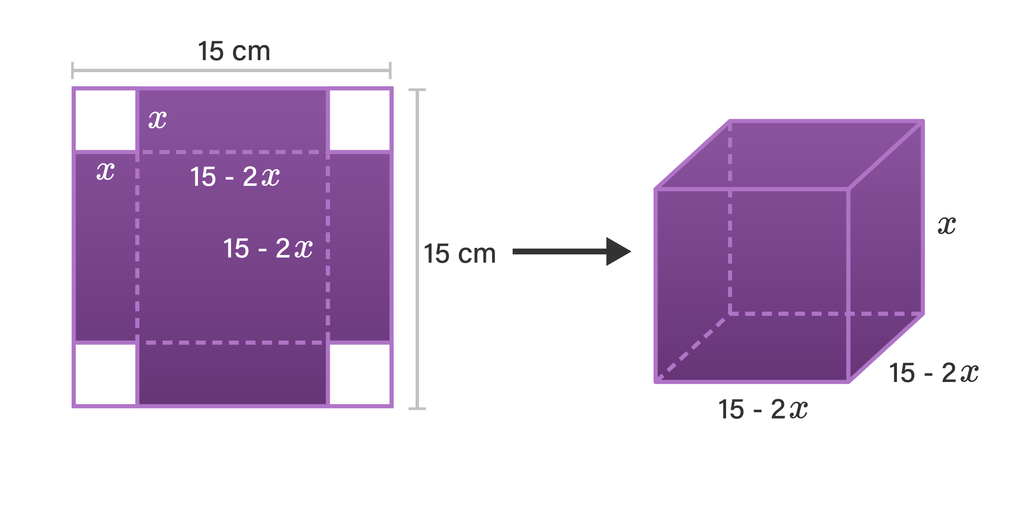
pak johan akan membuat cetakan kue. ia menggunakan bahan berupa lembaran logam berukuran 15 cm x 15 cm. pada keempat pojok logam digambar persegi berukuran x cm. selanjutnya, persegi-persegi tersebut dipotong. lembaran yang diperoleh ditekuk menjadi cetakan kue berbentuk balok. volume maksimum cetakan kue yang diperoleh adalah
3
1
Iklan
WL
W. Lestari
Mahasiswa/Alumni Universitas Sriwijaya
12 Maret 2022 10:10
Jawaban terverifikasi
Halo Adik. Terima kasih sudah bertanya di Roboguru. Jawaban : 250 cm³ Perhatikan penjelasan berikut ya. Ingat kembali: 1.) V = p x l x t dengan: V = volume balok p = panjang l = lebar t = tinggi 2.) f(x) = a → f'(x) = 0 3.) f(x) = ax → f'(x) = a 4.) f(x) = axⁿ → f'(x) = a.n.xⁿ¯¹ 5.) maksimum/minimum → f'(x) = 0 Diketahui : dari soal yang diberikan, dpaat diberika ilustrasi gambar seperti yang dilampirkan Ditanya : volume maksimum = ... ? Maka: p = (15 - 2x) karena panjang logam 15 cm, lalu digunting sebanyak x di kanan dan kirinya l = (15 - 2x) karena lebar logam 15 cm, lalu digunting sebanyak x di kanan dan kirinya t = (x) karena setelah digunting, logam ditekuk agar berbentuk balok V(x) = p x l x t V(x) = (15 - 2x) . (15 - 2x) . x V(x) = (225 - 30x - 30x + 4x²) . x V(x) = (225 - 60x + 4x²) . x V(x) = 225x - 60x² + 4x³ V(x) = 4x³ - 60x² + 225x Diperoleh: V(x) = 4x³ - 60x² + 225x V(x) = 4 . x³ - 60 . x² + 225x V'(x) = 4 . 3 . x³¯¹ - 60 . 2 . x²¯¹ + 225 V'(x) = 12 . x² - 120 . x + 225 V'(x) = 12x² - 120x + 225 maksimum/minimum → f'(x) = 0 V'(x) = 0 12x² - 120x + 225 = 0 4x² - 40x + 75 = 0 (2x - 15)(2x - 5) = 0 pembuat nol: 2x - 15 = 0 → x = 15/2 → tidak memenuhi karena ukuran sisi logam 15 cm, tidak mungkin ukuran sisi persegi yang dipotong 15/2 cm 2x - 5 = 0 → x = 5/2 → memenuhi Sehingga: V(x) = 4x³ - 60x² + 225x V(5/2) = 4.(5/2)³ - 60.(5/2)² + 225.(5/2) V(5/2) = 4.(125/8) - 60.(25/4) + 1.125/2 V(5/2) = 125/2 - 750/2 + 1.125/2 V(5/2) = 500/2 V(5/2) = 250 Jadi, volume cetakan maksimum adalah 250 cm³. Semoga membantu.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



