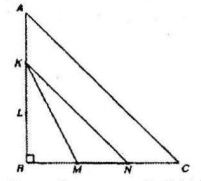
Pada segitiga siku-siku sama kaki ABC, sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, dan M, N. Jika luas ∆ABC adalah x cm², maka luas ∆KMN adalah ... cm². (A) x/3 (B) 2x/9 (C) x/9 (D) x/18 (E) x/36

<p>Jawaban yang benar adalah B. 2x/9.</p><p>&nbsp;</p><p>Diketahui:</p><p>Segitiga siku-siku sama kaki ABC.</p><p>Sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, dan M, N.</p><p>Luas ∆ABC adalah x cm².</p><p>&nbsp;</p><p>Ditanya:</p><p>Luas ∆KMN = ...?</p><p>&nbsp;</p><p>Jawab:</p><p>Konsep yang kita gunakan adalah luas segitiga. Luas segitiga dirumuskan oleh:</p><p>L = 1/2 x alas x tinggi.</p><p>&nbsp;</p><p>Dari gambar soal, luas ∆ABC dinyatakan oleh:</p><p>L ∆ABC = 1/2 . BC . AB</p><p>x = 1/2 . BC . AB</p><p>BC . AB = 2x ...(i)</p><p>&nbsp;</p><p>Dikarenakan sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, dan M, N sehingga diperoleh hubungan perbandingan berikut:</p><p>KB = (2/3) AB dan MN = (1/3) BC.</p><p>&nbsp;</p><p>Maka luas ∆KMN adalah:</p><p>L ∆KMN = 1/2 . MN . KB</p><p>L ∆KMN = 1/2 . (1/3) BC . (2/3) AB</p><p>L ∆KMN = 1/9 . BC . AB ...(ii)</p><p>&nbsp;</p><p>Substitusi persamaan (i) ke (ii) lalu diperoleh:</p><p>L ∆KMN = 1/9 . BC . AB</p><p>L ∆KMN = 1/9 . (2x)</p><p>L ∆KMN = (2x/9) cm².</p><p>&nbsp;</p><p>Oleh karena itu, jawaban yang benar adalah B.</p>