Keysha F
23 Februari 2023 12:39
Iklan
Keysha F
23 Februari 2023 12:39
Pertanyaan
Pada segitiga ABC diketahui: ∠A =45°, sisi a= 12 cm dan b = 12 cm. Panjang jari-jari lingkaran dalam segitiga ABC sama dengan ... a. (12- 6√2) cm b. (12 - 4√2) cm c. (8 - 4√3) cm d. (8-3√2) cm e. (8 - 6√2) cm
1
1
Iklan
P. Vidya
Mahasiswa/Alumni Universitas Negeri Malang
25 Mei 2023 03:15
<p>Halo Keysha. Kakak bantu jawab ya.</p><p>Jawab: A</p><p>Pembahasan:</p><p>Ingat!</p><p>Diketahui segitiga ABC. Rumus untuk menentukan panjang jari-jari lingkaran segitiga ABC adalah </p><p>r<sub>d</sub> = (Luas segitiga ABC)/(s)</p><p>dengan s adalah setengah keliling segitiga ABC.</p><p>Dengan menggunakan konsep di atas, diperoleh</p><p>Karena panjang sisi a sama dengan panjang sisi b, maka segitiga ABC adalah segitiga siku-siku. Oleh karena itu, besar sudut A dan besar sudut B adalah sama besar. Diperoleh </p><p>∠A = ∠B = 45°.</p><p>Karena jumlah sudut pada segitiga adalah 180°, maka</p><p>∠C = 180°-45°-45°</p><p> = 90°</p><p>Oleh karena itu, segitiga ABC adalah segitiga siku-siku dengan siku-siku di D.</p><p>Jika segitiga ABC diilustrasikan, diperoleh gambar seperti berikut.</p><p>Langkah 1. Menentukan luas segitiga ABC.</p><p>Luas segitiga ABC = 1/2 ×BC ×AC</p><p> = 1/2 ×12 ×12</p><p> = 72</p><p>Sehingga, luas segitiga ABC adalah 72 cm<sup>2</sup>.</p><p>Langkah 2. Menentukan setengah keliling segitiga ABC.</p><p>Menentukan panjang sisi AB.</p><p>Karena segitiga ABC adalah segitiga siku-siku dengan siku-siku di C, berlaku Teorema Pythagoras:</p><p>AB = √(AC<sup>2</sup>+BC<sup>2</sup>)</p><p> = √(12<sup>2</sup>+12<sup>2</sup>)</p><p> = √(288)</p><p> = 12√2</p><p>Sehingga, panjang sisi AB adalah 12√2 cm.</p><p>Setengah keliling segitiga ABC adalah </p><p>s = 1/2 (AB + BC + AC)</p><p> = 1/2 (12√2 + 12 + 12)</p><p> = 12+6√2</p><p>Sehingga, setengah keliling segitiga ABC adalah (12+6√2) cm.</p><p>Langkah 3. Menentukan panjang jari-jari lingkaran dalam segitiga ABC.</p><p>r<sub>d</sub> = (Luas segitiga ABC)/(s)</p><p> = 72/(12+6√2)</p><p> = 12/(2+√2)</p><p>Dirasionalkan dengan mengalikan pembilang dan penyebutnya dengan 2-√2. Diperoleh</p><p> 12/(2+√2) = 12/(2+√2) × (2-√2)/(2-√2)</p><p> = (24-12√2)/(4-2)</p><p> = (24-12√2)/(2)</p><p> = 12-6√2</p><p>Sehingga, panjang jari-jari lingkaran dalam segitiga ABC adalah (12-6√2) cm.</p><p> </p><p><strong><u>Jadi, jawaban yang benar adalah A.</u></strong></p>
Halo Keysha. Kakak bantu jawab ya.
Jawab: A
Pembahasan:
Ingat!
Diketahui segitiga ABC. Rumus untuk menentukan panjang jari-jari lingkaran segitiga ABC adalah
rd = (Luas segitiga ABC)/(s)
dengan s adalah setengah keliling segitiga ABC.
Dengan menggunakan konsep di atas, diperoleh
Karena panjang sisi a sama dengan panjang sisi b, maka segitiga ABC adalah segitiga siku-siku. Oleh karena itu, besar sudut A dan besar sudut B adalah sama besar. Diperoleh
∠A = ∠B = 45°.
Karena jumlah sudut pada segitiga adalah 180°, maka
∠C = 180°-45°-45°
= 90°
Oleh karena itu, segitiga ABC adalah segitiga siku-siku dengan siku-siku di D.
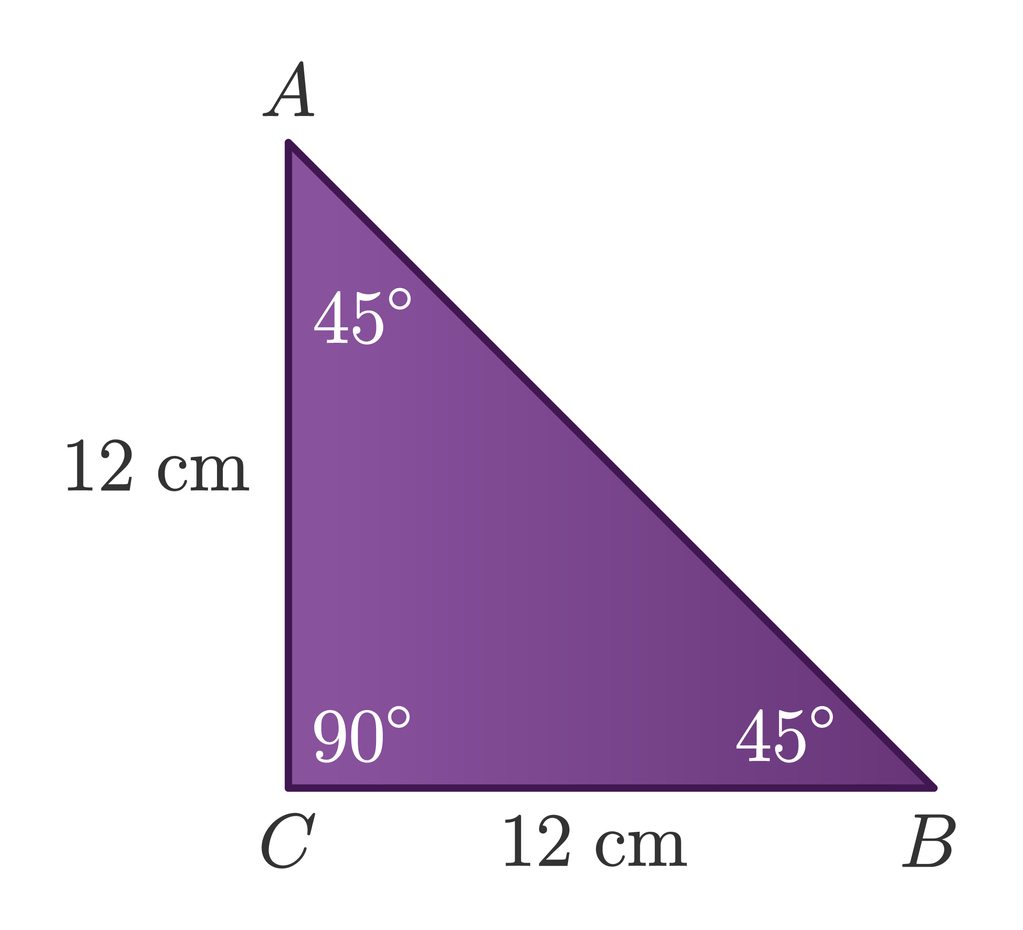
Jika segitiga ABC diilustrasikan, diperoleh gambar seperti berikut.
Langkah 1. Menentukan luas segitiga ABC.
Luas segitiga ABC = 1/2 ×BC ×AC
= 1/2 ×12 ×12
= 72
Sehingga, luas segitiga ABC adalah 72 cm2.
Langkah 2. Menentukan setengah keliling segitiga ABC.
Menentukan panjang sisi AB.
Karena segitiga ABC adalah segitiga siku-siku dengan siku-siku di C, berlaku Teorema Pythagoras:
AB = √(AC2+BC2)
= √(122+122)
= √(288)
= 12√2
Sehingga, panjang sisi AB adalah 12√2 cm.
Setengah keliling segitiga ABC adalah
s = 1/2 (AB + BC + AC)
= 1/2 (12√2 + 12 + 12)
= 12+6√2
Sehingga, setengah keliling segitiga ABC adalah (12+6√2) cm.
Langkah 3. Menentukan panjang jari-jari lingkaran dalam segitiga ABC.
rd = (Luas segitiga ABC)/(s)
= 72/(12+6√2)
= 12/(2+√2)
Dirasionalkan dengan mengalikan pembilang dan penyebutnya dengan 2-√2. Diperoleh
12/(2+√2) = 12/(2+√2) × (2-√2)/(2-√2)
= (24-12√2)/(4-2)
= (24-12√2)/(2)
= 12-6√2
Sehingga, panjang jari-jari lingkaran dalam segitiga ABC adalah (12-6√2) cm.
Jadi, jawaban yang benar adalah A.
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



