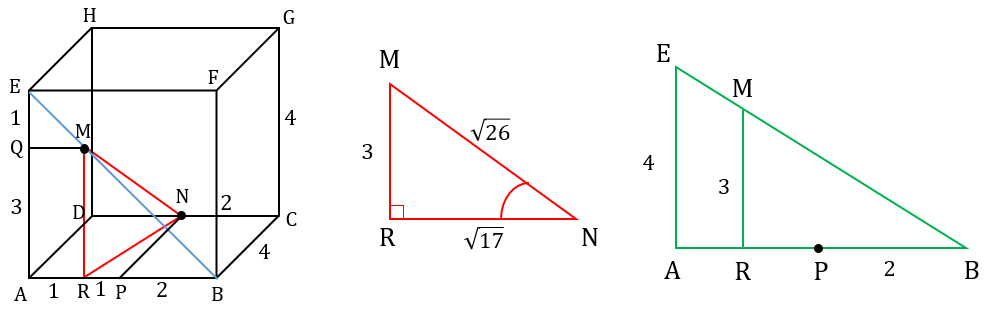
Pada kubus ABCD.EFGH, titik M terletak pada diagonal BE dengan perbandingan EM : MB = 1 : 3 dan N adalah titik tengah rusuk CD. Jika R terletak pada rusuk AB dimana RM sejajar AE, maka sin∠MNR adalah .... (A) √17/√26 (B) 2/√26 (C) 3/√26 (D) √5/√26 (E) 5/√26

Question

Jawaban yang benar adalah C. 3/√26.

Diketahui:

Kubus ABCD.EFGH

Titik M terletak pada diagonal BE

EM : MB = 1 : 3

N adalah titik tengah rusuk CD

R terletak pada rusuk AB dimana RM sejajar AE

Ditanya:

Nilai sin ∠MNR = ...?

Jawab:

(i). Definisi fungsi sinus yaitu: sin A = sisi depan/sisi miring.

(ii). Pada suatu segitiga siku-siku berlaku teorema Pythagoras yaitu:

c² = a² + b².

(iii). Dua bangun atau lebih dikatakan sebangun jika bentuknya sama tetapi ukurannya berbeda. Dua bangun datar yang sebangun memiliki ciri-ciri sebagai berikut:

(1). Sisi-sisi yang seletak atau bersesuaian adalah sebanding, artinya perbandingan panjang sisi-sisi itu sama.

(2) Sudut-sudut yang seletak atau bersesuaian adalah sama besar.

Keterangan:

a = sisi mendatar segitiga (cm)

b = sisi tegak segitiga (cm)

c = sisi miring segitiga (cm).

Berdasarkan gambar terlampir di bawah, dimisalkan panjang rusuk kubus adalah 4 satuan.

Selanjutnya perhatikan gambar segitiga hijau. Dengan konsep perbandingan diperoleh:

RB/AB = RM/AE

(RP+PB)/AB = RM/AE

(RP+2)/4 = 3/4

RP + 2 = 3

RP = 3 - 2

RP = 1 satuan.

Maka, garis AR yaitu: AR = AP - RP = 2 - 1 = 1 satuan.

Kemudian tinjau segitiga siku-siku RPN di dalam gambar kubus ABCD.EFGH sebelah kiri. Panjang garis RN pada segitiga RPN adalah:

RN² = RP² + PN²

RN² = (1)² + (4)²

RN² = 1 + 16

RN² = 17

RN = ±√17 satuan.

Ukuran panjang adalah positif, maka yang memenuhi adalah RN = √17 cm.

Kemudian perhatikan segitiga siku-siku MNR pada gambar kanan. Panjang garis MN pada segitiga MNR adalah:

MN² = MR² + RN²

MN² = (3)² + (√17)²

MN² = 9 + 17

MN² = 26

MN = ±√26 satuan.

Ukuran panjang adalah positif, maka yang memenuhi adalah RN = √26 cm.

Dari definisi sudut sinus diperoleh hasil:

sin ∠MNR = sisi depan / sisi miring

sin ∠MNR = MR/MN

sin ∠MNR = 3/√26.

Oleh karena itu, jawaban yang benar adalah C.

Pada kubus ABCD.EFGH, titik M terletak pada diagonal BE dengan perbandingan EM : MB = 1 : 3 dan N adalah titik tengah rusuk CD. Jika R terletak pada rusuk AB dimana RM sejajar AE, maka sin∠MNR adalah .... (A) √17/√26 (B) 2/√26 (C) 3/√26 (D) √5/√26 (E) 5/√26

Mau pemahaman lebih dalam untuk soal ini?

Pertanyaan serupa