VV
Valey V
27 April 2022 06:12
Iklan
VV
Valey V
27 April 2022 06:12
Pertanyaan
Nilai maksimum dari fungsi p=5000x+6000y pada himpunan penyelesaian sistem pertidaksamaan: x≥0; y≥0; 2x+y≤50; dan 3x+4y≤120 adalah … A. 172.500 B. 178.000 C. 180.000 D. 188.000 E. 189.000
1
1
Iklan
DN
D. Nuryani
Mahasiswa/Alumni Universitas Padjadjaran
27 Juli 2022 07:02
Jawaban terverifikasi
Jawaban : D. 188.000 Langkah-langkah mencari daerah penyelesaian SPtLDV: 1) Gambar masing-masing grafik 2) Uji titik untuk mencari daerah pertidaksamaan 3) Cari daerah yang beririsan dari kedua pertidaksamaan Kemudian untuk mencari nilai maksimum dari daerah penyelesaian dapat digunakan metode titik pojok (menyubstitusikan titik pojok pada fungsi objektif). Diketahui SPtLDV x≥0; y≥0; 2x+y≤50; 3x+4y≤120 Fungsi Objektif : p=5000x+6000y Pertama, gambarkan grafiknya Grafik 2x + y = 50 ▪️ Titik potong sumbu X, y = 0 2x + y = 50 2x + 0 = 50 2x = 50 x = 25 (25, 0) ▪️ Titik potong sumbu Y, x = 0 2x + y = 50 2(0) + y = 50 y = 50 (0, 50) Uji daerah pada titik (0, 0) 2x+y≤50 0 + 0 ≤ 50 0 ≤ 50 (benar) sehingga daerah penyelesaian 2x+y≤50 melewati titik (0,0) Grafik 3x + 4y = 120 ▪️ Titik potong sumbu X, y = 0 3x + 4y = 120 3x + 0 = 120 3x = 120 x = 40 (40, 0) ▪️ Titik potong sumbu Y, x = 0 3x + 4y = 120 0 + 4y = 120 4y = 120 y = 30 (0, 30) Uji daerah pada titik (0, 0) 3x+4y≤120 0 + 0 ≤ 120 0 ≤ 120 (benar) sehingga daerah penyelesaian 3x+4y≤120 melewati titik (0,0) Gambarkan daerah penyelesaian pada bidang kartesius (dilampirkan) Kemudian cari titik potong kedua garis 2x + y = 50 |x4| 3x + 4y = 120 |x1| ______________ 8x + 4y = 200 3x + 4y = 120 - ______________ 5x = 80 x = 80/5 x = 16 Substitusi x= 16 ke 2x + y = 50 2x + y = 50 2(16) + y = 50 32 + y = 50 y = 50 -32 y = 18 (16, 18) Diperoleh berdasarkan gambar bahwa titik pojoknya adalah (0,0) ---> p=5000(0)+6000(0) = 0 (0, 30) ---> p=5000(0)+6000(30) = 180.000 (25, 0) ---> p=5000(25)+6000(0) = 125.000 (16, 18) ---> p=5000(16)+6000(18) = 188.000 Nilai maksimumnya adalah 188.000. Jadi, nilai maksimum untuk soal di atas adalah 188.000
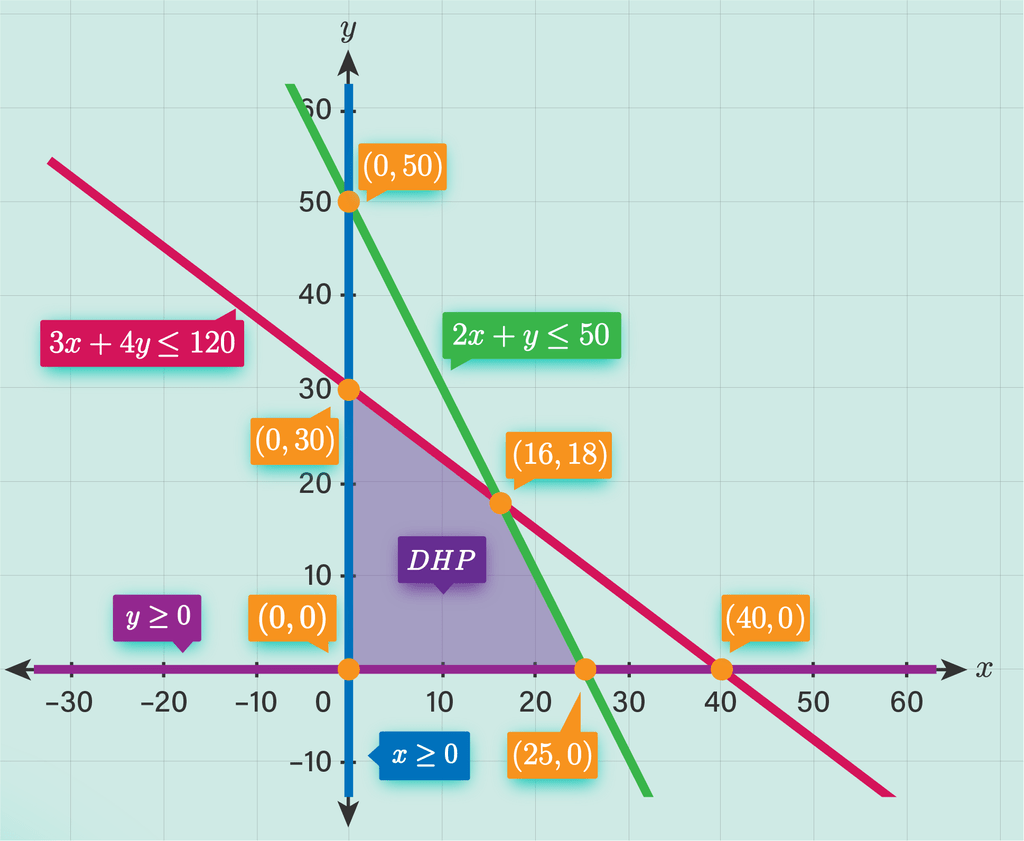
· 5.0 (1)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



