Luas daerah penyelesaian sistem pertidaksamaan 3x+2y ≥ 6,3x+2y ≤ 12, dan 0 ≤ y ≤ 3 adalah ....

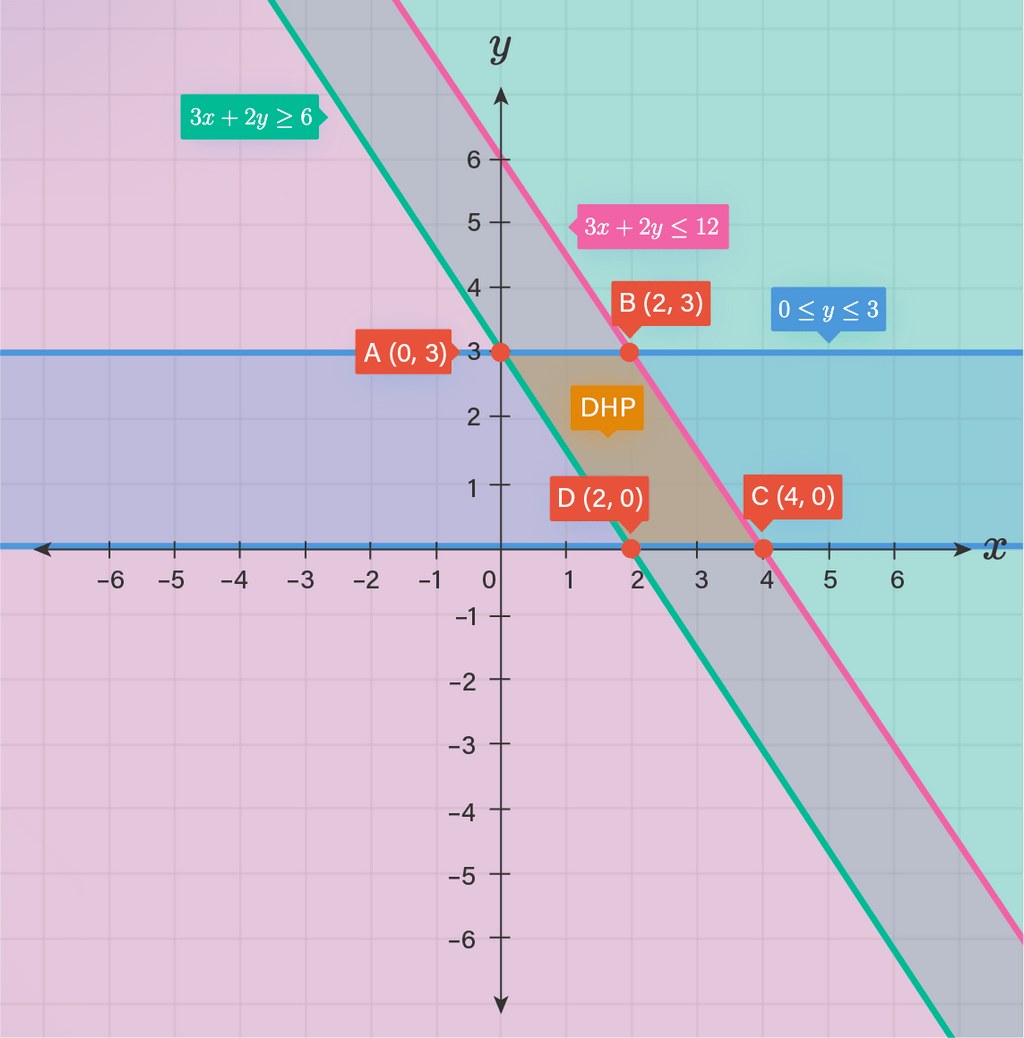
Hai Niko, terima kasih sudah bertanya di Roboguru. Kakak bantu jawab ya :) Luas daerah penyelesaian dari sistem pertidaksamaan 3x+2y ≥ 6, 3x+2y ≤ 12, dan 0 ≤ y ≤ 3 adalah 6 satuan persegi. Pada soal diberikan sistem pertidaksamaan seperti berikut : {3x + 2y ≥ 6 {3x + 2y ≤ 12 {0 ≤ y ≤ 3 Pertidaksamaan pertama 3x + 2y ≥ 6 merupakan sebuah garis lurus yang melalui titik : Untuk x = 0 3(0) + 2y = 6 2y = 6 y = 3 Untuk y = 0 3x + 2(0) = 6 3x = 6 x = 2 Maka garis lurus 3x + 2y = 6 melalui titik (2, 0) dan (0, 3). Dengan uji titik, apabila disubtitusikan (0, 0) maka pertidaksamaan 3(0) + 2(0) = 0 ≥ 6 bernilai salah. Sehingga daerah yang diarsir adalah daerah yang tidak memuat (0, 0) yaitu daerah di sebelah kanan/atas garis. Pertidaksamaan kedua 3x + 2y ≤ 12 merupakan sebuah garis lurus yang melalui titik : Untuk x = 0 3(0) + 2y = 12 2y = 12 y = 6 Untuk y = 0 3x +2(0) = 12 3x = 12 x = 4 Maka garis lurus 3x + 2y = 12 melalui titik (4, 0) dan (0, 6). Dengan uji titik, apabila disubtitusikan (0, 0) maka pertidaksamaan 3(0) + 2(0) = 0 ≤ 12 bernilai benar. Sehingga daerah yang diarsir adalah daerah yang memuat (0, 0), yaitu daerah di sebelah kiri/bawah garis. Pertidaksamaan ketiga 0 ≤ y ≤ 3 merupakan sebuah daerah di tengah antara garis sumbu y = 0 dan y = 3. Apabila ketiga pertidaksamaan tersebut digambarkan, maka akan terbentuk titik potong dan batas daerah penyelesaiannya (DHP). Titik-titik tersebut antara lain : A(0, 3), B(2, 3), C(4, 0), dan D(2, 0), yang membentuk suatu jajargenjang. Alas jajar genjang adalah ruas garis CD, yang panjangnya adalah jarak antara titik C(4, 0) dan titik D(2, 0). Dengan rumus jarak dapat dihitung : alas = √((x₂ - x₁)² + (y₂ - y₁)²) alas = √((4 - 2)² + (0 - 0)²) alas = √((2²) + 0) alas = √4 alas = 2 satuan Tinggi jajar genjang adalah garis BD, yang panjangnya adalah jarak antara titik B(2, 3) dan titik D(2, 0). tinggi = √((x₂ - x₁)² + (y₂ - y₁)²) tinggi = √((2 - 2)² + (3 - 0)²) tinggi = √((0)² + (3)²) tinggi = √9 tinggi = 3 satuan Sehingga luas jajargenjang ABCD adalah Luas = alas × tinggi Luas = CD × BD Luas = 2 × 3 Luas = 6 satuan persegi. Jadi, luas jajargenjang yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah 6 satuan persegi. Ilustrasi daerah penyelesaian dapat kamu lihat pada gambar di bawah ini ya. Semoga membantu ya, Niko. Semangat Belajar! :)