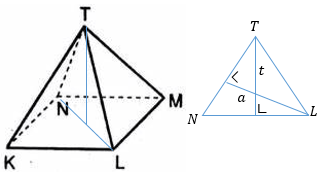
Limas beraturan T.KLMN mempunyai panjang rusuk alas 6 cm dan rusuk tegak 8 cm. Jarak antara titik L dan rusuk TN adalah ....

<p>Jawaban : (3√(23))/2 cm</p><p>&nbsp;</p><p>Ingat!&nbsp;</p><p>Pada limas dengan alas berbentuk persegi, untuk mencari tinggi prisma dapat digunakan rumus&nbsp;</p><p>t = √(st²-(d/2)²)</p><p>d = s√2</p><p>dengan&nbsp;</p><p>s : sisi alas</p><p>t : tinggi limas</p><p>st : panjang sisi tegak</p><p>d : diagonal persegi</p><p>Jarak titik ke garis adalah panjang ruas garis terpendek yang menghubungkan garis dan titik tersebut.</p><p>Luas segitiga = 1/2 x alas x tinggi</p><p>&nbsp;</p><p>Diketahui Limas beraturan T.KLMN dengan</p><p>st = 8 cm</p><p>s = 6 cm</p><p>&nbsp;</p><p>Sehingga</p><p>d = s√2</p><p>d = 6√2 cm</p><p>&nbsp;</p><p>t = √(st²-(d/2)²)</p><p>t = √(8²-(6√2/2)²)</p><p>t = √(8²-(3√2)²)</p><p>t = √(64-18)</p><p>t = √(46) cm</p><p>&nbsp;</p><p>Pada segitiga TNL dengan</p><p>NL = 6√2 cm</p><p>TN = TL = 8 cm</p><p>&nbsp;</p><p>Jika alas segitiga TNL adalah NL, maka tinggi segitiga = t = √(46) cm.</p><p>Jika alas segitiga TNL adalah TN, maka tinggi segitiga = a</p><p>dengan a adalah jarak titik L ke garis TN.</p><p>&nbsp;</p><p>Dengan menggunakan luas segitiga TNL diperoleh</p><p>luas TNL = luas TNL</p><p>1/2 . NL . t = 1/2 . TN . a</p><p>NL . t = TN . a</p><p>6√2 . √(46) = 8 . a</p><p>6√(92) = 8 . a</p><p>6.2√(23) = 8 . a</p><p>12√(23) = 8 . a</p><p>(3√(23))/2 = a</p><p>&nbsp;</p><p>Jadi, Jarak antara titik L dan rusuk TN adalah (3√(23))/2 cm</p>