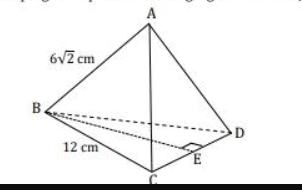
Limas ABCD pada gambar di samping merupakan limas segitiga beraturan. Jarak titik A ke garis BE adalah .... A. 3√(2)cm B. 2√(6)cm C. 6cm D. 4√(3)cm E. 8cm

<p>Jawaban : 2√6 cm.</p><p>&nbsp;</p><p>Pembahasan :</p><p>Konsep :</p><p>Jarak titik ke garis adalah panjang garis ke proyeksi titik tersebut pada garis.</p><p>Pythagoras :</p><p>a = √(c² − b²)</p><p>dimana</p><p>c : sisi miring</p><p>a, b : sisi yang saling tegak lurus</p><p>Pada segitiga ABC, P adalah titik berat dan O adala titik tengah BC, maka AP = 2/3 AO</p><p>&nbsp;</p><p>Perhatikan gambar.</p><p>CD = 12 cm</p><p>E titik tengah CD, maka</p><p>CE = 1/2 CD</p><p>= 1/2 (12)</p><p>= 6 cm</p><p>&nbsp;</p><p>BE = √(BC² − CE²)</p><p>= √(12² − 6²)</p><p>= √(144 − 36)</p><p>= √(108)</p><p>= √(36×3)</p><p>= 6√3 cm</p><p>&nbsp;</p><p>H titik berat BCD</p><p>BH = 2/3 BE</p><p>= 2/3 (6√3)</p><p>= 4√3 cm</p><p>&nbsp;</p><p>AH tegak lurus BH</p><p>AH = √(AB² − BH²)</p><p>= √((6√2)² − (4√3)²)</p><p>= √(72 − 48)</p><p>= √(24)</p><p>= √(4×6)</p><p>= 2√6 cm</p><p>&nbsp;</p><p>Jarak titik A ke garis BE = AH = 2√6 cm</p><p>&nbsp;</p><p>Jadi, Jarak titik A ke garis BE adalah 2√6 cm.</p>