Bintang B
21 Agustus 2023 17:27
Iklan
Bintang B
21 Agustus 2023 17:27
Pertanyaan
lim x -> 0 (sin^2 (3x))/(2cos 2x - 2)
lim x -> 0 (sin^2 (3x))/(2cos 2x - 2)
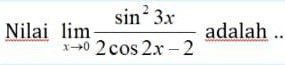
1
1
Iklan
Ipan G
22 Agustus 2023 02:02
<p><strong>Untuk menjawab soal tersebut anda perlu memahami tentang identitas sudut rangkap trigonometri</strong></p><p><strong>lim x--> 0 sin²(3x)/(2cos(2x) - 2)</strong></p><p><strong>Faktorkan 2cos(2x) - 2 menjadi 2(cos(2x) - 1)</strong></p><p><strong>= lim x--> 0 sin²(3x)/(2(cos(2x) - 1))</strong></p><p> </p><p><strong>Kemudian menggunakan identitas sudut rangkap ubah menjadi :</strong></p><p><strong>cos(2x) = 1 - 2sin²(x)</strong></p><p><strong>Sehingga : </strong></p><p><strong>cos(2x) - 1 = -2sin²(x)</strong></p><p> </p><p><strong>= lim x--> 0 sin²(3x)/(2(-2sin²(x))</strong></p><p><strong>= lim x--> 0 sin²(3x)/(-4sin²(x))</strong></p><p><strong>= [lim x--> 0 sin(3x)/-4sin(x)] × lim x--> sin(3x)/sin(x)</strong></p><p><strong>= -3/4 × 3 = -9/4</strong></p><p><strong>Semoga membantu!</strong></p><p> </p>
Untuk menjawab soal tersebut anda perlu memahami tentang identitas sudut rangkap trigonometri
lim x--> 0 sin²(3x)/(2cos(2x) - 2)
Faktorkan 2cos(2x) - 2 menjadi 2(cos(2x) - 1)
= lim x--> 0 sin²(3x)/(2(cos(2x) - 1))
Kemudian menggunakan identitas sudut rangkap ubah menjadi :
cos(2x) = 1 - 2sin²(x)
Sehingga :
cos(2x) - 1 = -2sin²(x)
= lim x--> 0 sin²(3x)/(2(-2sin²(x))
= lim x--> 0 sin²(3x)/(-4sin²(x))
= [lim x--> 0 sin(3x)/-4sin(x)] × lim x--> sin(3x)/sin(x)
= -3/4 × 3 = -9/4
Semoga membantu!
· 5.0 (1)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



