Ohhh A
31 Juli 2024 02:05
Iklan
Ohhh A
31 Juli 2024 02:05
Pertanyaan
lim sin 3x sin 7x / 4x² x~0
1
2
Iklan
BimBim B
31 Juli 2024 07:36
<h2>Jawabannya adalah 21/4.</h2><p> </p><p><strong><u>Penjelasan</u></strong></p><p>terlampir</p>
Jawabannya adalah 21/4.
Penjelasan
terlampir
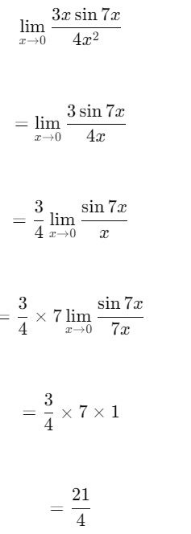
· 5.0 (1)
Iklan
Nanda R

Community
31 Juli 2024 21:27
<p>Untuk menghitung limit dari fungsi \(\frac{\sin(3x) \sin(7x)}{4x^2}\) saat \(x\) mendekati 0, kita bisa menggunakan beberapa aturan dasar limit dan identitas trigonometri. Mari kita uraikan langkah-langkahnya:</p><p>1. **Gunakan Identitas Trigonometri**:<br> Kita dapat menggunakan identitas trigonometri untuk menyederhanakan bentuk \(\sin(3x) \sin(7x)\). Identitas yang berguna di sini adalah:</p><p> \[<br> \sin A \sin B = \frac{1}{2} [\cos(A - B) - \cos(A + B)]<br> \]</p><p> Dengan \(A = 3x\) dan \(B = 7x\):</p><p> \[<br> \sin(3x) \sin(7x) = \frac{1}{2} [\cos(3x - 7x) - \cos(3x + 7x)]<br> \]</p><p> \[<br> \sin(3x) \sin(7x) = \frac{1}{2} [\cos(-4x) - \cos(10x)]<br> \]</p><p> Karena \(\cos(-4x) = \cos(4x)\), maka:</p><p> \[<br> \sin(3x) \sin(7x) = \frac{1}{2} [\cos(4x) - \cos(10x)]<br> \]</p><p>2. **Hitung Limit**:<br> Substitusi ke dalam limit:</p><p> \[<br> \lim_{x \to 0} \frac{\sin(3x) \sin(7x)}{4x^2} = \lim_{x \to 0} \frac{\frac{1}{2} [\cos(4x) - \cos(10x)]}{4x^2}<br> \]</p><p> \[<br> = \frac{1}{8} \lim_{x \to 0} \frac{\cos(4x) - \cos(10x)}{x^2}<br> \]</p><p> Kita dapat menggunakan fakta bahwa \(\cos(4x)\) dan \(\cos(10x)\) mendekati 1 saat \(x \to 0\), sehingga:</p><p> \[<br> \cos(4x) - \cos(10x) \approx -10x \sin(10x) + 4x \sin(4x)<br> \]</p><p> Sekarang, gunakan deret Taylor untuk \(\cos\) sekitar \(x = 0\):</p><p> \[<br> \cos(x) \approx 1 - \frac{x^2}{2}<br> \]</p><p> Maka:</p><p> \[<br> \cos(4x) \approx 1 - \frac{(4x)^2}{2} = 1 - 8x^2<br> \]</p><p> \[<br> \cos(10x) \approx 1 - \frac{(10x)^2}{2} = 1 - 50x^2<br> \]</p><p> \[<br> \cos(4x) - \cos(10x) \approx (1 - 8x^2) - (1 - 50x^2) = 42x^2<br> \]</p><p> Jadi:</p><p> \[<br> \frac{\cos(4x) - \cos(10x)}{x^2} \approx 42<br> \]</p><p> Maka:</p><p> \[<br> \lim_{x \to 0} \frac{\sin(3x) \sin(7x)}{4x^2} = \frac{1}{8} \times 42 = \frac{21}{4}<br> \]</p><p> Jadi, limitnya adalah \(\frac{21}{4}\).</p>
Untuk menghitung limit dari fungsi \(\frac{\sin(3x) \sin(7x)}{4x^2}\) saat \(x\) mendekati 0, kita bisa menggunakan beberapa aturan dasar limit dan identitas trigonometri. Mari kita uraikan langkah-langkahnya:
1. **Gunakan Identitas Trigonometri**:
Kita dapat menggunakan identitas trigonometri untuk menyederhanakan bentuk \(\sin(3x) \sin(7x)\). Identitas yang berguna di sini adalah:
\[
\sin A \sin B = \frac{1}{2} [\cos(A - B) - \cos(A + B)]
\]
Dengan \(A = 3x\) dan \(B = 7x\):
\[
\sin(3x) \sin(7x) = \frac{1}{2} [\cos(3x - 7x) - \cos(3x + 7x)]
\]
\[
\sin(3x) \sin(7x) = \frac{1}{2} [\cos(-4x) - \cos(10x)]
\]
Karena \(\cos(-4x) = \cos(4x)\), maka:
\[
\sin(3x) \sin(7x) = \frac{1}{2} [\cos(4x) - \cos(10x)]
\]
2. **Hitung Limit**:
Substitusi ke dalam limit:
\[
\lim_{x \to 0} \frac{\sin(3x) \sin(7x)}{4x^2} = \lim_{x \to 0} \frac{\frac{1}{2} [\cos(4x) - \cos(10x)]}{4x^2}
\]
\[
= \frac{1}{8} \lim_{x \to 0} \frac{\cos(4x) - \cos(10x)}{x^2}
\]
Kita dapat menggunakan fakta bahwa \(\cos(4x)\) dan \(\cos(10x)\) mendekati 1 saat \(x \to 0\), sehingga:
\[
\cos(4x) - \cos(10x) \approx -10x \sin(10x) + 4x \sin(4x)
\]
Sekarang, gunakan deret Taylor untuk \(\cos\) sekitar \(x = 0\):
\[
\cos(x) \approx 1 - \frac{x^2}{2}
\]
Maka:
\[
\cos(4x) \approx 1 - \frac{(4x)^2}{2} = 1 - 8x^2
\]
\[
\cos(10x) \approx 1 - \frac{(10x)^2}{2} = 1 - 50x^2
\]
\[
\cos(4x) - \cos(10x) \approx (1 - 8x^2) - (1 - 50x^2) = 42x^2
\]
Jadi:
\[
\frac{\cos(4x) - \cos(10x)}{x^2} \approx 42
\]
Maka:
\[
\lim_{x \to 0} \frac{\sin(3x) \sin(7x)}{4x^2} = \frac{1}{8} \times 42 = \frac{21}{4}
\]
Jadi, limitnya adalah \(\frac{21}{4}\).
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



