Roboguru
SD
SMP
SMA
UTBK/SNBT

Dwi S

07 Oktober 2024 13:09

Iklan

Dwi S

07 Oktober 2024 13:09

Pertanyaan

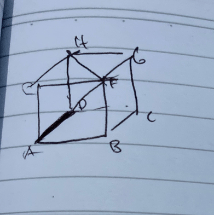
kubus ABCD EFGH dengan rusuk 11cm jarak titik A ke bidang DHF adalah

kubus ABCD EFGH dengan rusuk 11cm jarak titik A ke bidang DHF adalah

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

01

:

21

:

10

:

54

Klaim

2

2

Jawaban terverifikasi

Iklan

Rendi R

Community

07 Oktober 2024 13:55

Jawaban terverifikasi

<p>Untuk mencari jarak dari titik AAA ke bidang DHFDHFDHF pada kubus dengan panjang rusuk 11 cm, berikut langkah-langkah penyelesaiannya tanpa menggunakan simbol matematika yang kompleks.</p><p>Langkah-langkah:</p><p><strong>Identifikasi posisi titik dan bidang pada kubus:</strong></p><ul><li>Panjang rusuk kubus adalah 11 cm.</li><li>Titik AAA berada di sudut A dari kubus. Secara sederhana, bisa kita posisikan titik AAA ini di koordinat (0, 0, 0).</li><li>Bidang DHFDHFDHF merupakan bidang yang melalui tiga titik yaitu D, H, dan F. Berdasarkan posisi kubus:<ul><li>Titik D berada pada (11, 0, 0).</li><li>Titik H berada pada (11, 11, 11).</li><li>Titik F berada pada (0, 11, 11).</li></ul></li></ul><p><strong>Cari persamaan bidang DHF:</strong></p><ul><li>Untuk mencari persamaan bidang, kita memerlukan dua vektor yang berada di bidang tersebut.</li><li>Vektor pertama dapat diperoleh dari titik D ke titik H, yaitu dengan mengurangkan koordinat titik H dari koordinat titik D, hasilnya adalah (-11, 11, 11).</li><li>Vektor kedua dapat diperoleh dari titik D ke titik F, hasilnya juga (-11, 11, 11).</li><li>Kemudian, kita hitung vektor normal dengan melakukan perkalian silang (cross product) dari dua vektor tersebut. Hasilnya adalah sebuah vektor yang tegak lurus terhadap bidang tersebut.</li></ul><p><strong>Hitung jarak titik A ke bidang DHF:</strong></p><ul><li>Setelah kita mendapatkan vektor normal bidang, kita dapat mencari jarak dari titik A ke bidang dengan menggunakan rumus jarak titik ke bidang. Diketahui posisi titik A dan persamaan bidang yang terbentuk, kita substitusi nilai ke rumus untuk menghitung jaraknya.</li></ul><p>Jadi, jarak titik A ke bidang DHF pada kubus tersebut adalah 11 cm.</p>

Untuk mencari jarak dari titik AAA ke bidang DHFDHFDHF pada kubus dengan panjang rusuk 11 cm, berikut langkah-langkah penyelesaiannya tanpa menggunakan simbol matematika yang kompleks.

Langkah-langkah:

Identifikasi posisi titik dan bidang pada kubus:

  • Panjang rusuk kubus adalah 11 cm.
  • Titik AAA berada di sudut A dari kubus. Secara sederhana, bisa kita posisikan titik AAA ini di koordinat (0, 0, 0).
  • Bidang DHFDHFDHF merupakan bidang yang melalui tiga titik yaitu D, H, dan F. Berdasarkan posisi kubus:
    • Titik D berada pada (11, 0, 0).
    • Titik H berada pada (11, 11, 11).
    • Titik F berada pada (0, 11, 11).

Cari persamaan bidang DHF:

  • Untuk mencari persamaan bidang, kita memerlukan dua vektor yang berada di bidang tersebut.
  • Vektor pertama dapat diperoleh dari titik D ke titik H, yaitu dengan mengurangkan koordinat titik H dari koordinat titik D, hasilnya adalah (-11, 11, 11).
  • Vektor kedua dapat diperoleh dari titik D ke titik F, hasilnya juga (-11, 11, 11).
  • Kemudian, kita hitung vektor normal dengan melakukan perkalian silang (cross product) dari dua vektor tersebut. Hasilnya adalah sebuah vektor yang tegak lurus terhadap bidang tersebut.

Hitung jarak titik A ke bidang DHF:

  • Setelah kita mendapatkan vektor normal bidang, kita dapat mencari jarak dari titik A ke bidang dengan menggunakan rumus jarak titik ke bidang. Diketahui posisi titik A dan persamaan bidang yang terbentuk, kita substitusi nilai ke rumus untuk menghitung jaraknya.

Jadi, jarak titik A ke bidang DHF pada kubus tersebut adalah 11 cm.

Iklan

Javas A

07 Oktober 2024 15:31

Jawaban terverifikasi

<p>Jawabannya 11CM,Karena:</p><p>Bidang DFH merupakan gabungan dari titik d , f, dan h</p><p>maka dari itu jarak terdekat dari titik a ke bidang DFH adalah jarak titik a ke titik d yang dimana itu merupakan rusuk =11 Cm,Semoga membantu terimakasih</p>

Jawabannya 11CM,Karena:

Bidang DFH merupakan gabungan dari titik d , f, dan h

maka dari itu jarak terdekat dari titik a ke bidang DFH adalah jarak titik a ke titik d yang dimana itu merupakan rusuk =11 Cm,Semoga membantu terimakasih

alt

Mau pemahaman lebih dalam untuk soal ini?

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS

LATIHAN SOAL GRATIS!

Drill Soal

Latihan soal sesuai topik yang kamu mau untuk persiapan ujian

Cobain Drill Soal

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

Gold Icon

Klaim Gold gratis sekarang!

Dengan Gold kamu bisa tanya soal ke Forum sepuasnya, lho.

Pertanyaan serupa

Sebuah mobil dengan harga awal Rp. 200.000.000,00 yang mengalami penurunan harga sebesar Rp. 15.000.000 setiap tahunnyya. Tentukan harga mobil setelah 5 tahun?

32

5.0

Jawaban terverifikasi

1. penyebab perubahan sosial budaya yang berasal dari masyarakat yang berkaitan demografi 2. penyebab perubahan sosial budaya yang terkait dengan fenomena globalisasi 3. Tanda-tanda sikap mental masyarakat yang belum siap menerima kemajuan teknologi 4. Dampak modernisasi dalam kehidupan sosial masyarakat 5. Kegiatan manusia di bidang ekonomi yang menunjukkan perubahan ke arah modernisasi 6. Contoh pengaruh modernisasi di bidang ilmu pengetahuan dan pendidikan terhadap pola pikir masyarakat 7. Konsep mengenai proses modernisasi di masyarakat seringkali mengalami kesalahan pahaman, salah satunya kesalahan tersebut menganggap jika menjadi modern adalah mengikuti... 8. arti dari globalisasi 9. Bentuk kearifan lokal di wilayah Madura yang berperan dalam pengelolaan SDA dan dukungan dalam bentuk kebudayaan 10. Syarat menjaga tradisi kearifan lokal di Nusantara 11. Ciri uang kartal, giral 12. Syarat melakukan kegiatan barter 13. Arti dari durability yang merupakan syarat sebuah benda bisa dikatakan sebagai uang 14. maksud token money dalam nilai intrinsik 15. maksud dengan satuan hitung dalam fungsi uang 16. fungsi uang 17. peranan dan maksud didirikan lembaga keuangan non-Bank / bukan bank 18. maksud dengan kegiatan menghimpun dana yang dilakukan perbankan 19. tugas Bank Indonesia 20. tugas Bank Umum 21. kegiatan lembaga keuangan non-Bank 22. kelembagaan keuangan non-bank yang memiliki kegiatan yang dilakukan dengan operasi simpan pinjam 23. Lembaga keuangan non bank yang memiliki fungsi sebagai penggerak investasi dengan memperhatikan dan memasukan surat berharga 24. Nama lembaga keuangan non bank yang bertugas mengatasi para rensumen 25. Ciri" dari masyarakat ekonomi abad ke 21

12

5.0

Jawaban terverifikasi

Iklan

hitunglah panjang tali busur QT dan panjang OR, jika jari jarinya adalah 14cm

7

0.0

Jawaban terverifikasi

pusat lingkaran x²+y²-4=0 adalah

246

5.0

Jawaban terverifikasi

tinggi dan berat badan seorang wanita memiliki hubungan linier yang dapat dimodelkan y = 1,2 X + 96 dengan X mewakili berat badan ideal dalam kg dan Y mewakili tinggi dalam cm. Berapakah berat badan ideal seorang wanita yang memiliki tinggi badan 156 cm

4

4.0

Jawaban terverifikasi