Aulia R
27 Februari 2023 02:28
Iklan
Aulia R
27 Februari 2023 02:28
Pertanyaan
Himpunan penyelesaian dari: cos(2x + 30°) ≥ 1 pada interval 0°≤ x ≤ 180° adalah ... A. {x I 0° ≤ x ≤ 15° atau 135° ≤ x ≤ 180° } B. {x I 15° ≤ x ≤ 30° atau 135° ≤ x ≤ 180° } c. {x I 120 °≤ x ≤ 180°} D. {x I 15° ≤ x ≤ 150°} , E. {x I 15° ≤ x ≤ 30° atau 120°≤ x ≤ 135°}
2
1
Iklan
C. Salsa
Mahasiswa/Alumni Universitas Gajah Mada
07 Maret 2023 12:13
<p>Jawaban : {165°}</p><p> </p><p>Ingat!</p><p>Persamaan trigonometri bentuk cos: </p><p>cos x = cos a </p><p>maka x = ±a + k·360°</p><p>k bilangan bulat </p><p> </p><p>Diketahui cos(2x + 30°) ≥ 1</p><p> </p><p>Pembuat nol :</p><p>cos(2x + 30°) = 1</p><p>cos(2x + 30°) = cos 0°</p><p>2x+30° = ±0° + k·360°</p><p>2x+30° = k·360° </p><p>2x = -30° + k·360° </p><p>x = -15° + k·180°</p><p>dengan k bilangan bulat.</p><p> </p><p>Untuk x = 0, maka</p><p>x = -15° + 0·180°</p><p>x = -15° + 0°</p><p>x = -15° </p><p> </p><p>Untuk x = 1, maka</p><p>x = -15° + 1·180°</p><p>x = -15° + 180°</p><p>x = 165° </p><p> </p><p>Karena 0° ≤ x ≤ 180°, maka diperoleh yang x = 165°</p><p> </p><p>Uji titik :</p><p>Untuk 0° ≤ x ≤ 165°, dipilih x = 30°, maka cos(60° + 30°) = cos 90° = 0 < 1 </p><p>Untuk 165° ≤ x ≤ 180°, dipilih x = 170°, maka cos(340° + 30°) = cos 370° = cos 10° < 1 </p><p>Karena cos(2x + 30°) ≥ 1, maka dipilih positif, Diperoleh</p><p>x = 165°</p><p> </p><p>Jadi, Himpunan penyelesaian dari cos(2x + 30°) ≥ 1 pada interval 0°≤ x ≤ 180° adalah {165°}</p><p>tidak pilihan jawaban yang benar</p>
Jawaban : {165°}
Ingat!
Persamaan trigonometri bentuk cos:
cos x = cos a
maka x = ±a + k·360°
k bilangan bulat
Diketahui cos(2x + 30°) ≥ 1
Pembuat nol :
cos(2x + 30°) = 1
cos(2x + 30°) = cos 0°
2x+30° = ±0° + k·360°
2x+30° = k·360°
2x = -30° + k·360°
x = -15° + k·180°
dengan k bilangan bulat.
Untuk x = 0, maka
x = -15° + 0·180°
x = -15° + 0°
x = -15°
Untuk x = 1, maka
x = -15° + 1·180°
x = -15° + 180°
x = 165°
Karena 0° ≤ x ≤ 180°, maka diperoleh yang x = 165°
Uji titik :
Untuk 0° ≤ x ≤ 165°, dipilih x = 30°, maka cos(60° + 30°) = cos 90° = 0 < 1
Untuk 165° ≤ x ≤ 180°, dipilih x = 170°, maka cos(340° + 30°) = cos 370° = cos 10° < 1
Karena cos(2x + 30°) ≥ 1, maka dipilih positif, Diperoleh
x = 165°
Jadi, Himpunan penyelesaian dari cos(2x + 30°) ≥ 1 pada interval 0°≤ x ≤ 180° adalah {165°}
tidak pilihan jawaban yang benar
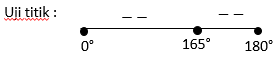
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



