Alyssa A
31 Juli 2023 12:51
Iklan
Alyssa A
31 Juli 2023 12:51
Pertanyaan
hasil dari limit x mendekati 0 untuk 4x/sin 2x + tan 3x
12
2
Iklan
HIZKIA Z

Community
08 Oktober 2023 10:34
<p>Semoga membantu ya...</p>
Semoga membantu ya...
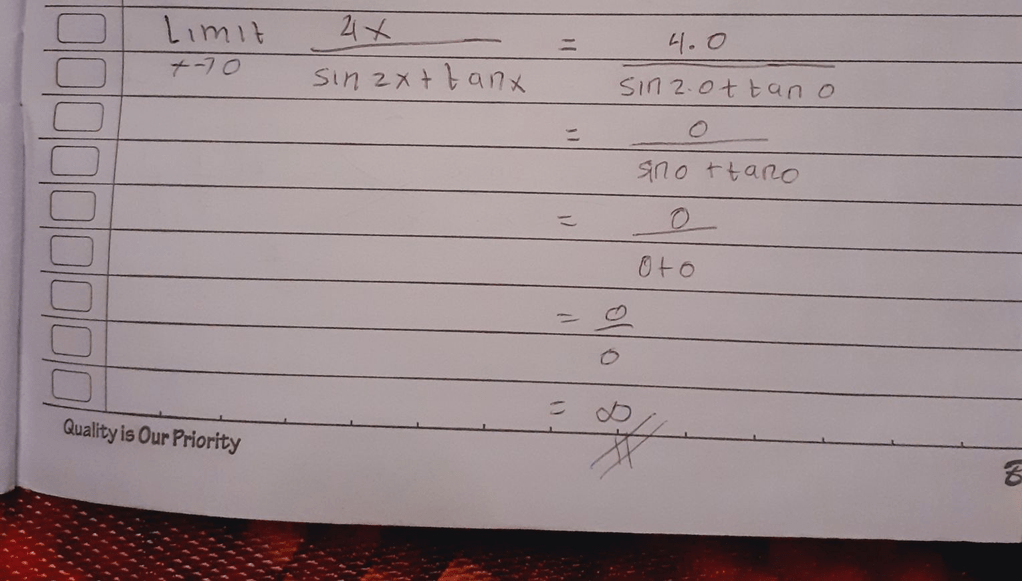
· 5.0 (1)
Iklan
DosenMuu D
09 Agustus 2023 14:53
<p>Untuk mencari nilai dari limit saat x mendekati 0 dari fungsi (4x/sin 2x) + tan 3x, kita dapat menggunakan aturan L'Hôpital atau menggunakan pendekatan aljabar.</p><p>Menggunakan aturan L'Hôpital:<br>Diferensiasi pada pembilang dan penyebut dapat dilakukan secara terpisah, dan kemudian mengambil limit dari hasilnya saat x mendekati 0.</p><p>f(x) = (4x/sin 2x) + tan 3x</p><p>*f'(x) = (4/sin(2x)) * 2 + (sec^2(3x)) * 3 = (8/sin(2x)) + 3sec^2(3x)</p><p>Langkah pertama, kita hitung limit pembilang dan penyebut saat x mendekati 0:</p><p>lim (x→0) [8/sin(2x)] = 8/sin(0) = 8/0 (tidak terdefinisi)</p><p>lim (x→0) [3sec^2(3x)] = 3sec^2(0) = 3(1) = 3</p><p>Karena limit pembilang tidak terdefinisi, dan limit penyebut memiliki nilai 3, maka limit dari fungsi (4x/sin 2x) + tan 3x saat x mendekati 0 tidak ada (tidak terdefinisi).</p><p>Menggunakan pendekatan aljabar:<br>Kita dapat membagi setiap suku dengan x dan kemudian mengambil limit saat x mendekati 0:</p><p>f(x) = (4x/sin 2x) + tan 3x<br> = 4(sin 3x)/(sin 2x) + tan 3x</p><p>Langkah pertama, kita bagi setiap suku dengan x:</p><p>f(x) = (4(sin 3x)/(sin 2x)) * (1/x) + (tan 3x) * (x/x)<br> <br>Kemudian, kita dapat mengambil limit saat x mendekati 0:</p><p>lim (x→0) [(4(sin 3x)/(sin 2x)) * (1/x)] + [(tan 3x) * (x/x)]<br>= lim (x→0) [(4sin 3x)/(xsin 2x)] + lim (x→0) [(tan 3x)]</p><p>Kita telah mengubah bentuk aslinya menjadi dua limit terpisah.</p><p>Untuk limit pertama, dapat dinyatakan sebagai:</p><p>lim (x→0) [(4sin 3x)/(xsin 2x)] = 0/0 (bentuk tidak terdefinisi)</p><p>Untuk limit kedua, dapat ditentukan sebagai:</p><p>lim (x→0) [(tan 3x)] = tan(0) = 0</p><p>Karena limit pertama tidak terdefinisi, dan limit kedua memiliki nilai 0, maka limit dari fungsi (4x/sin 2x) + tan 3x saat x mendekati 0 juga tidak ada (tidak terdefinisi).</p><p>Kesimpulannya, limit (4x/sin 2x) + tan 3x saat x mendekati 0 tidak ada (tidak terdefinisi).</p>
Untuk mencari nilai dari limit saat x mendekati 0 dari fungsi (4x/sin 2x) + tan 3x, kita dapat menggunakan aturan L'Hôpital atau menggunakan pendekatan aljabar.
Menggunakan aturan L'Hôpital:
Diferensiasi pada pembilang dan penyebut dapat dilakukan secara terpisah, dan kemudian mengambil limit dari hasilnya saat x mendekati 0.
f(x) = (4x/sin 2x) + tan 3x
*f'(x) = (4/sin(2x)) * 2 + (sec^2(3x)) * 3 = (8/sin(2x)) + 3sec^2(3x)
Langkah pertama, kita hitung limit pembilang dan penyebut saat x mendekati 0:
lim (x→0) [8/sin(2x)] = 8/sin(0) = 8/0 (tidak terdefinisi)
lim (x→0) [3sec^2(3x)] = 3sec^2(0) = 3(1) = 3
Karena limit pembilang tidak terdefinisi, dan limit penyebut memiliki nilai 3, maka limit dari fungsi (4x/sin 2x) + tan 3x saat x mendekati 0 tidak ada (tidak terdefinisi).
Menggunakan pendekatan aljabar:
Kita dapat membagi setiap suku dengan x dan kemudian mengambil limit saat x mendekati 0:
f(x) = (4x/sin 2x) + tan 3x
= 4(sin 3x)/(sin 2x) + tan 3x
Langkah pertama, kita bagi setiap suku dengan x:
f(x) = (4(sin 3x)/(sin 2x)) * (1/x) + (tan 3x) * (x/x)
Kemudian, kita dapat mengambil limit saat x mendekati 0:
lim (x→0) [(4(sin 3x)/(sin 2x)) * (1/x)] + [(tan 3x) * (x/x)]
= lim (x→0) [(4sin 3x)/(xsin 2x)] + lim (x→0) [(tan 3x)]
Kita telah mengubah bentuk aslinya menjadi dua limit terpisah.
Untuk limit pertama, dapat dinyatakan sebagai:
lim (x→0) [(4sin 3x)/(xsin 2x)] = 0/0 (bentuk tidak terdefinisi)
Untuk limit kedua, dapat ditentukan sebagai:
lim (x→0) [(tan 3x)] = tan(0) = 0
Karena limit pertama tidak terdefinisi, dan limit kedua memiliki nilai 0, maka limit dari fungsi (4x/sin 2x) + tan 3x saat x mendekati 0 juga tidak ada (tidak terdefinisi).
Kesimpulannya, limit (4x/sin 2x) + tan 3x saat x mendekati 0 tidak ada (tidak terdefinisi).
· 0.0 (0)
Mau jawaban yang terverifikasi?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



