Gayatri N
06 Oktober 2023 12:33
Iklan
Gayatri N
06 Oktober 2023 12:33
Pertanyaan
Haloo mohon bantuannya ya terimakasih Gambarlah grafik fungsi kuadrat beserta cara atau tahapannya dari y= -x^2-2x+8
Haloo mohon bantuannya ya terimakasih
Gambarlah grafik fungsi kuadrat beserta cara atau tahapannya dari y= -x^2-2x+8
1
1
Iklan
Bagir S
06 Oktober 2023 16:11
<p>Halo! Fungsi kuadrat yang diberikan adalah y = -x^2 - 2x + 8. Untuk menggambar grafiknya, kita perlu menentukan titik-titik penting yang akan membantu kita merencanakan kurva.</p><p>1. Titik Potong dengan sumbu X:<br> Untuk mencari titik potong dengan sumbu X, kita set y = 0 dan mencari nilai-nilai x yang membuat persamaan menjadi nol.<br> 0 = -x^2 - 2x + 8<br> Mari kita faktorkan persamaan di atas menjadi:<br> 0 = -(x^2 + 2x - 8)<br> Aljabar tidak memiliki faktor (x + a) (x + b) di mana a dan b menghasilkan -2 ketika ditambahkan dan -8 ketika dikalikan. Oleh karena itu, kita akan menggunakan rumus kuadrat untuk mencari akar-akarnya.<br> x = (-b ± √(b^2 - 4ac)) / 2a<br> a = 1, b = -2, c = 8<br> Dengan mengganti nilai-nilai tersebut ke dalam rumus, kita dapat mencari dua nilai x:<br> x = (-(-2) ± √((-2)^2 - 4(1)(8))) / (2(1))<br> x = (2 ± √(4 - 32)) / 2<br> x = (2 ± √(-28)) / 2<br> x = (2 ± 2i√7) / 2<br> x = 1 ± i√7</p><p> Akan tetapi, karena kita sedang mencari titik potong dengan sumbu X, kita hanya tertarik pada solusi nyata. Maka, dalam kasus ini, tidak ada titik potong dengan sumbu X dan kurva akan terletak di atas sumbu X.</p><p>2. Vertex (Puncak):<br> Untuk mencari koordinat vertex atau puncak parabola, kita dapat menggunakan rumus x = -b / (2a).</p><p> x = -(-2) / (2*1)<br> x = 2 / 2<br> x = 1<br> Substitusikan nilai x = 1 ke dalam persamaan asli untuk mencari nilai y:<br> y = -(1)^2 - 2(1) + 8<br> y = -1 - 2 + 8<br> y = 5</p><p> Jadi, koordinat vertex atau puncak parabola adalah (1, 5).</p><p>Dengan titik-titik penting ini, kita dapat menggambar kurva fungsi kuadrat. Parabola akan cekung ke bawah karena koefisien depan x^2 yaitu -1 negatif.</p><p>Menggunakan info yang kita miliki:<br>- Tidak ada titik potong dengan sumbu X.<br>- Puncak adalah (1, 5).</p><p>Berikut adalah ilustrasi grafik fungsi kuadrat y = -x^2 - 2x + 8:<br> </p>
Halo! Fungsi kuadrat yang diberikan adalah y = -x^2 - 2x + 8. Untuk menggambar grafiknya, kita perlu menentukan titik-titik penting yang akan membantu kita merencanakan kurva.
1. Titik Potong dengan sumbu X:
Untuk mencari titik potong dengan sumbu X, kita set y = 0 dan mencari nilai-nilai x yang membuat persamaan menjadi nol.
0 = -x^2 - 2x + 8
Mari kita faktorkan persamaan di atas menjadi:
0 = -(x^2 + 2x - 8)
Aljabar tidak memiliki faktor (x + a) (x + b) di mana a dan b menghasilkan -2 ketika ditambahkan dan -8 ketika dikalikan. Oleh karena itu, kita akan menggunakan rumus kuadrat untuk mencari akar-akarnya.
x = (-b ± √(b^2 - 4ac)) / 2a
a = 1, b = -2, c = 8
Dengan mengganti nilai-nilai tersebut ke dalam rumus, kita dapat mencari dua nilai x:
x = (-(-2) ± √((-2)^2 - 4(1)(8))) / (2(1))
x = (2 ± √(4 - 32)) / 2
x = (2 ± √(-28)) / 2
x = (2 ± 2i√7) / 2
x = 1 ± i√7
Akan tetapi, karena kita sedang mencari titik potong dengan sumbu X, kita hanya tertarik pada solusi nyata. Maka, dalam kasus ini, tidak ada titik potong dengan sumbu X dan kurva akan terletak di atas sumbu X.
2. Vertex (Puncak):
Untuk mencari koordinat vertex atau puncak parabola, kita dapat menggunakan rumus x = -b / (2a).
x = -(-2) / (2*1)
x = 2 / 2
x = 1
Substitusikan nilai x = 1 ke dalam persamaan asli untuk mencari nilai y:
y = -(1)^2 - 2(1) + 8
y = -1 - 2 + 8
y = 5
Jadi, koordinat vertex atau puncak parabola adalah (1, 5).
Dengan titik-titik penting ini, kita dapat menggambar kurva fungsi kuadrat. Parabola akan cekung ke bawah karena koefisien depan x^2 yaitu -1 negatif.
Menggunakan info yang kita miliki:
- Tidak ada titik potong dengan sumbu X.
- Puncak adalah (1, 5).
Berikut adalah ilustrasi grafik fungsi kuadrat y = -x^2 - 2x + 8:
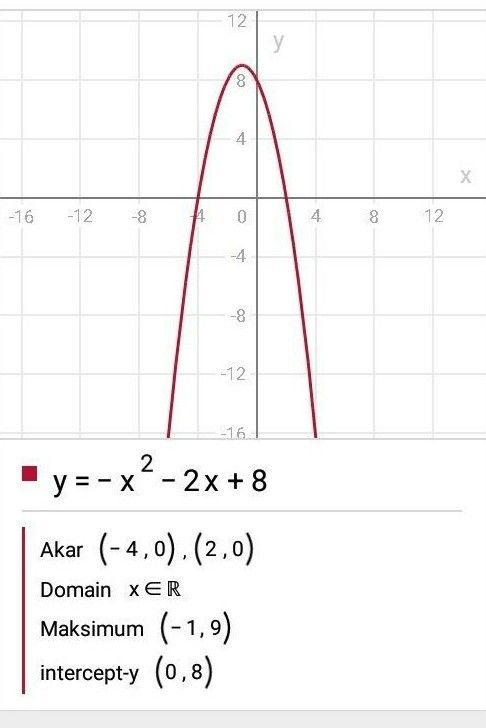
· 0.0 (0)
Gayatri N
07 Oktober 2023 00:39
terimakasih
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



