Fatima N
09 Juni 2022 05:54
Iklan
Fatima N
09 Juni 2022 05:54
Pertanyaan
Gambarlah kurva dan tentukan domain serta range dari fungsi berikut! 3. f(x) = (x² − 2x − 3)/(x² − 4)
21
1
Iklan
T. Teaching.Assistant.Yosi
21 Desember 2022 07:07
<p>Jawaban : Lihat Lampiran.</p><p>Df = {x|x ≠ 2 atau x ≠ -2, x∈R}</p><p>Rf = {y|y∈R}</p><p> </p><p>Pembahasan :</p><p>Diketahui f(x) = (x² − 2x − 3)/(x² − 4)</p><p>Gunakan konsep fungsi rasional.</p><p>1) Domain fungsi rasional adalah penyebut ≠ 0.</p><p>x² − 4 ≠ 0</p><p>(x - 2)(x + 2) ≠ 0</p><p>x ≠ 2 atau x ≠ -2</p><p>Df = {x|x ≠ 2 atau x ≠ -2, x∈R}</p><p>2) Gambar kurva</p><p>- Menentukan asimtot tegak (penyebut = 0)</p><p>x² − 4 = 0</p><p>(x - 2)(x + 2) = 0</p><p>x = 2 atau x = -2</p><p>- Menentukan asimtot datar (lim x–∞ f(x))</p><p>y = lim x–∞ (x² − 2x − 3)/(x² − 4)</p><p>y = 1</p><p>- Menentukan titik potong dengan sumbu Y (x = 0)</p><p>f(0) = (0² − 2(0) − 3)/(0² − 4) = 3/4</p><p>titik potong dengna sumbu Y di titik (0,3/4)</p><p>- Menentukan titik potong dengan sumbu X (y = 0)</p><p>0 = (x² − 2x − 3)/(x² − 4)</p><p>0 = x² − 2x − 3</p><p>0 = (x - 3)(x + 1)</p><p>x = 3 atau x = -1</p><p>titik potong dengan sumbu Y ada di titik (3,0) dan (-1,0)</p><p>Gambar lihat pada lampiran.</p><p>3) Range dari fungsi rasional</p><p>Rf = {y|y∈R}</p><p> </p><p>Jadi kurva dan tentukan domain serta range dari fungsi fx) terlihat pada lampiran.</p>
Jawaban : Lihat Lampiran.
Df = {x|x ≠ 2 atau x ≠ -2, x∈R}
Rf = {y|y∈R}
Pembahasan :
Diketahui f(x) = (x² − 2x − 3)/(x² − 4)
Gunakan konsep fungsi rasional.
1) Domain fungsi rasional adalah penyebut ≠ 0.
x² − 4 ≠ 0
(x - 2)(x + 2) ≠ 0
x ≠ 2 atau x ≠ -2
Df = {x|x ≠ 2 atau x ≠ -2, x∈R}
2) Gambar kurva
- Menentukan asimtot tegak (penyebut = 0)
x² − 4 = 0
(x - 2)(x + 2) = 0
x = 2 atau x = -2
- Menentukan asimtot datar (lim x–∞ f(x))
y = lim x–∞ (x² − 2x − 3)/(x² − 4)
y = 1
- Menentukan titik potong dengan sumbu Y (x = 0)
f(0) = (0² − 2(0) − 3)/(0² − 4) = 3/4
titik potong dengna sumbu Y di titik (0,3/4)
- Menentukan titik potong dengan sumbu X (y = 0)
0 = (x² − 2x − 3)/(x² − 4)
0 = x² − 2x − 3
0 = (x - 3)(x + 1)
x = 3 atau x = -1
titik potong dengan sumbu Y ada di titik (3,0) dan (-1,0)
Gambar lihat pada lampiran.
3) Range dari fungsi rasional
Rf = {y|y∈R}
Jadi kurva dan tentukan domain serta range dari fungsi fx) terlihat pada lampiran.
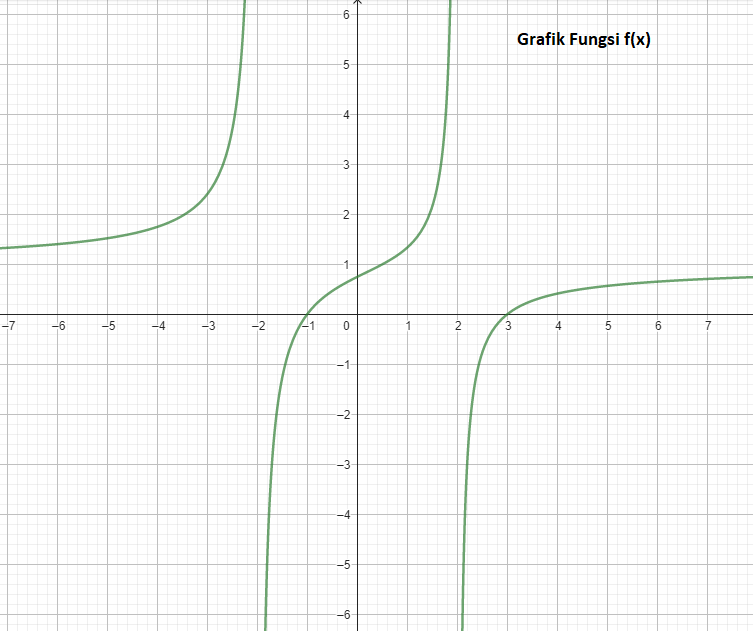
· 0.0 (0)
Iklan
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke Forum
Biar Robosquad lain yang jawab soal kamu

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



