Aira A

08 April 2023 03:14
Iklan
Aira A

08 April 2023 03:14
Pertanyaan
Gambarlah grafik dari persamaan fungsi kuadrat berikut : y = x² + 16x - 17
Gambarlah grafik dari persamaan fungsi kuadrat berikut : y = x² + 16x - 17
1
2
Iklan
Sumber W

Community
08 April 2023 04:57
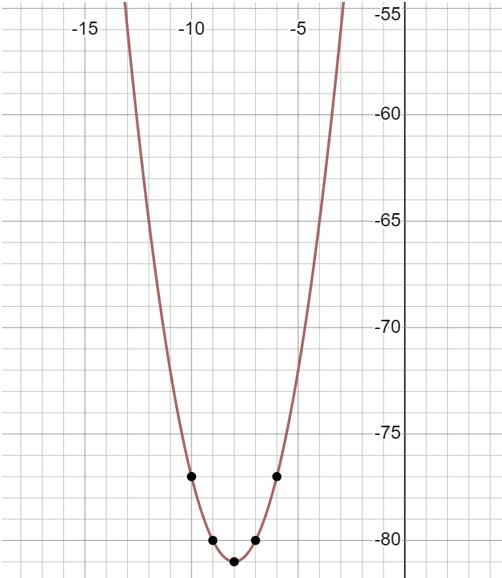
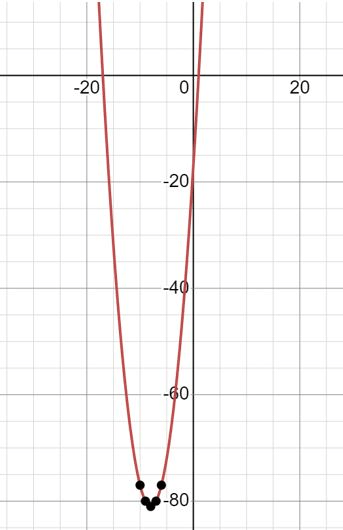
<p>y = x² + 16x - 17 </p><p><strong>Langkah 1 </strong>: Mencari titik potong sumbu x, maka y = 0</p><p>x² + 16x - 17 = 0</p><p>(x - 1)(x + 17) = 0</p><p>x<sub>1</sub> = 1 atau x<sub>2</sub> = -17</p><p>Grafik memotong sumbu x di (1,0) dan (-17,0)</p><p> </p><p><strong>Langkah 2 </strong> : Mencari titik potong sumbu y, maka x = 0</p><p>y = x² + 16x - 17 </p><p>y = (0)² + 16(0) - 17 </p><p>y = -17</p><p>Grafik memotong sumbu y di (0,-17)</p><p> </p><p><strong>Langkah 3</strong> : Mencari sumbu simetri dan titik puncak (titik minimum)</p><p>y = x² + 16x - 17 </p><p>a = 1; b = 16 dan c = -17</p><p>Sumbu simetri (x<sub>p</sub>) = -b/2a</p><p> = -16/2(1)</p><p> = -16/2</p><p> = -8 </p><p>y<sub>p </sub>= (b<sup>2</sup> - 4ac)/(-4a)</p><p> = (16<sup>2</sup> - 4(1)(-17))/(-4(1))</p><p> = (256 + 68)/-4</p><p> = 324/-4</p><p> = -81</p><p>Titik puncak = (x<sub>p</sub>,y<sub>p</sub>)</p><p> = (-8, -81)</p><p> </p><p>Gambarnya ada dibawah : </p><p> </p>
y = x² + 16x - 17
Langkah 1 : Mencari titik potong sumbu x, maka y = 0
x² + 16x - 17 = 0
(x - 1)(x + 17) = 0
x1 = 1 atau x2 = -17
Grafik memotong sumbu x di (1,0) dan (-17,0)
Langkah 2 : Mencari titik potong sumbu y, maka x = 0
y = x² + 16x - 17
y = (0)² + 16(0) - 17
y = -17
Grafik memotong sumbu y di (0,-17)
Langkah 3 : Mencari sumbu simetri dan titik puncak (titik minimum)
y = x² + 16x - 17
a = 1; b = 16 dan c = -17
Sumbu simetri (xp) = -b/2a
= -16/2(1)
= -16/2
= -8
yp = (b2 - 4ac)/(-4a)
= (162 - 4(1)(-17))/(-4(1))
= (256 + 68)/-4
= 324/-4
= -81
Titik puncak = (xp,yp)
= (-8, -81)
Gambarnya ada dibawah :
· 5.0 (1)
Iklan
Nanda R

Community
08 April 2023 03:43
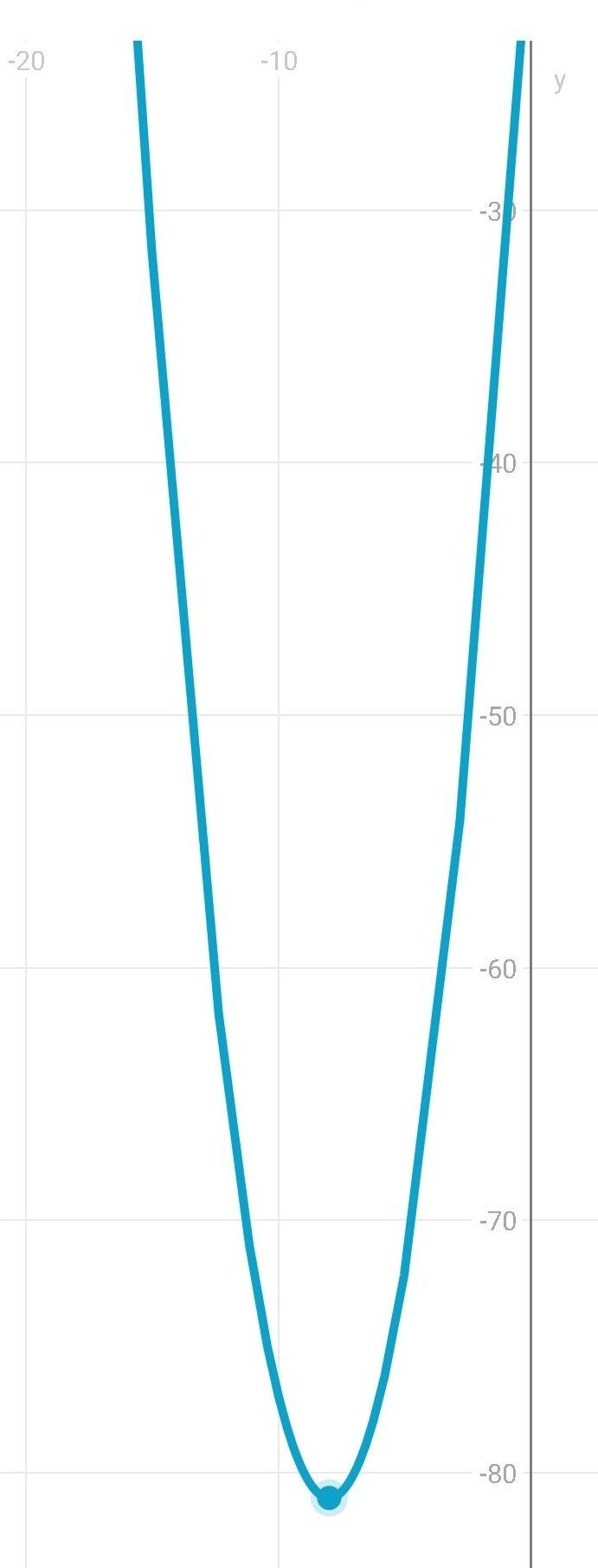
<p>akar persamaan : (-17,0) dan (1,0)</p><p>titik puncak : (-8,-81)</p>
akar persamaan : (-17,0) dan (1,0)
titik puncak : (-8,-81)
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



