Muhammad R
11 Januari 2023 04:57
Iklan
Muhammad R
11 Januari 2023 04:57
Pertanyaan
Gambarkan grafik fungsi berikut: 4. f(x)=x^(2)+2x
6
1
Iklan
M. Claudia
Master Teacher
Mahasiswa/Alumni Universitas Nusa Cendana Kupang
26 Januari 2023 05:25
<p>Jawaban yang benar adalah pada gambar terlampir.</p><p> </p><p>Ingat!</p><p>Grafik fungsi kuadrat ax² + bx + c terbuka ke atas apabila a > 0.</p><p>Grafik fungsi kuadrat ax² + bx + c terbuka ke bawah apabila a < 0.<br>Langkah-langkah untuk menentukan kurva grafik fungsi kuadrat sebagai berikut:<br>- menentukan titik potong pada sb.x<br>- menentukan titik potong pada sb.y<br>- menentukan titik puncak<br>- gambarkan<br>Rumus untuk menentukan titik puncak persamaan kuadrat ax² + bx + c adalah:<br>x<sub>p</sub> = −(b/2a) dan y<sub>p</sub> = −(b² − 4ac/4a).</p><p> </p><p>Berdasarkan soal,<br>Diketahui: f(x) = x² + x berarti a = 1, b = 1 , c = 0 </p><p>Karena a > 0 maka grafik terbuka ke atas.<br>Sebelum menggambar kurva fungsi f(x) = x² + 2x terlebih dahulu ditentukan titik-titiknya, diperoleh sebagai berikut:<br>f(x) = x² + 2x<br>- Untuk titik potong pada sb.x<br>f(x) = x² + 2x<br>0 = x² + 2x<br>x² + 2x = 0<br>x(x+2) = 0<br>x = 0<br>atau<br>x+2 = 0<br>x = −2<br>diperoleh titik (−2, 0) atau (0, 0)<br>- Untuk titik potong pada sb.y<br>y = f(x) = x² + 2x<br>y = f(x) = 0² + 2·0<br>y = f(x) = 0<br>diperoleh titik (0, 0).<br>- Untuk titik puncak<br>x<sub>p</sub> = −(b/2a)<br>x<sub>p</sub> = −(2/2(1))<br>x<sub>p</sub> = −1<br>maka nilai y<sub>p</sub><br>y<sub>p</sub> = −(b² − 4ac/4a)<br>y<sub>p</sub> = −((2)² − 4(1·0)/4(1))<br>y<sub>p</sub> = −((4−0)/4)<br>y<sub>p</sub> = −1<br>Jadi, titik puncaknya adalah (−1, −1)</p><p><br>Dengan menghubungkan semua titik-titiknya maka diperoleh grafik seperti pada gambar terlampir.</p><p>Dengan demikian, kurva dari fungsi y = f(x) adalah pada gambar terlampir.</p><p> </p><p>Semoga membantu ya🙂</p>
Jawaban yang benar adalah pada gambar terlampir.
Ingat!
Grafik fungsi kuadrat ax² + bx + c terbuka ke atas apabila a > 0.
Grafik fungsi kuadrat ax² + bx + c terbuka ke bawah apabila a < 0.
Langkah-langkah untuk menentukan kurva grafik fungsi kuadrat sebagai berikut:
- menentukan titik potong pada sb.x
- menentukan titik potong pada sb.y
- menentukan titik puncak
- gambarkan
Rumus untuk menentukan titik puncak persamaan kuadrat ax² + bx + c adalah:
xp = −(b/2a) dan yp = −(b² − 4ac/4a).
Berdasarkan soal,
Diketahui: f(x) = x² + x berarti a = 1, b = 1 , c = 0
Karena a > 0 maka grafik terbuka ke atas.
Sebelum menggambar kurva fungsi f(x) = x² + 2x terlebih dahulu ditentukan titik-titiknya, diperoleh sebagai berikut:
f(x) = x² + 2x
- Untuk titik potong pada sb.x
f(x) = x² + 2x
0 = x² + 2x
x² + 2x = 0
x(x+2) = 0
x = 0
atau
x+2 = 0
x = −2
diperoleh titik (−2, 0) atau (0, 0)
- Untuk titik potong pada sb.y
y = f(x) = x² + 2x
y = f(x) = 0² + 2·0
y = f(x) = 0
diperoleh titik (0, 0).
- Untuk titik puncak
xp = −(b/2a)
xp = −(2/2(1))
xp = −1
maka nilai yp
yp = −(b² − 4ac/4a)
yp = −((2)² − 4(1·0)/4(1))
yp = −((4−0)/4)
yp = −1
Jadi, titik puncaknya adalah (−1, −1)
Dengan menghubungkan semua titik-titiknya maka diperoleh grafik seperti pada gambar terlampir.
Dengan demikian, kurva dari fungsi y = f(x) adalah pada gambar terlampir.
Semoga membantu ya🙂
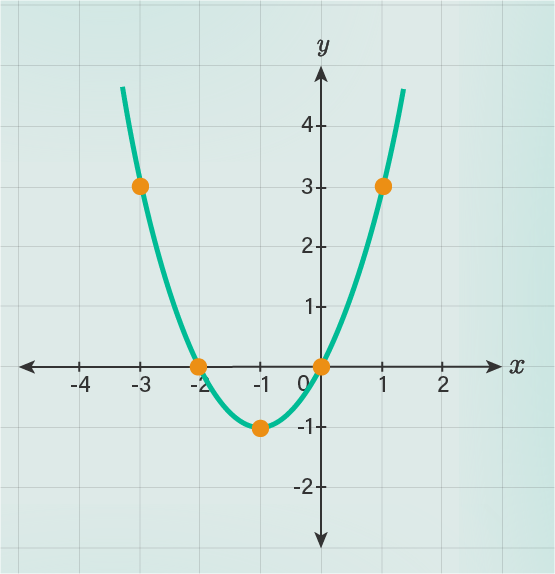
· 0.0 (0)
Iklan
Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia













