WS
Winda S
03 Januari 2022 14:13
Iklan
WS
Winda S
03 Januari 2022 14:13
Pertanyaan
Fungsi f(x)=2cos2x pada interval 0°<x<180°akan naik pada interval .... A. 0°<x<45° B. 0°<x<90° C. 30°<x<90° D. 60°<x<180° E. 90°<x<180°
14
2
Iklan
NS
N. Supriyaningsih
Mahasiswa/Alumni Universitas Kristen Satya Wacana
20 Maret 2022 11:32
Jawaban terverifikasi
Halo Winda, Kakak akan bantu jawab yaa :) Jawaban : E Ingat kembali, - Suatu fungsi f(x) akan naik pada saat f'(x)>0, dimana f'(x) adalah turunan pertama dari f(x) - Turunan dari cos nx = -n . sin nx - Penyelesaian dari sin x = sin A adalah x = A + k.360⁰ x = (180⁰-A) + k.360⁰ Diketahui: f(x) = 2 cos 2x , pada interval 0⁰≤x≤180⁰ Maka diperoleh f'(x) = 2 (-sin 2x) (2) f'(x) = -4 sin 2x Didapat titik-titik stasioner berikut f'(x) = 0 -4 sin 2x = 0 sin 2x = 0 sin 2x = sin 0⁰ Untuk 2x = 0⁰ + k.360⁰, maka x = 0⁰ + k. 180⁰ Saat k=0, maka x = 0⁰ (Tidak memenuhi) Saat k=1, maka x = 180⁰ (Tidak memenuhi) Untuk 2x = (180⁰- 0⁰) + k.360⁰, maka x = 90⁰ + k.180⁰ Saat k=0, maka x = 90⁰ Saat k=1, maka x = 270⁰ (Tidak memenuhi) Sehingga nilai x yang memenuhi adalah {90⁰} Untuk mengetahui interval naik, maka kita akan menguji nilai x yang memenuhi ke dalam f'(x). Untuk 0⁰<x<90⁰, maka ambil x = 60⁰ f'(60⁰) = -4 sin 2(60⁰) f'(60⁰) = -4 sin 120⁰ f'(60⁰) = -4(√3/2) f'(60⁰) = -2√3 Karena f'(60⁰) < 0, maka fungsi f(x) turun pada interval 0⁰<x<90⁰. Untuk 90⁰<x<180⁰, ambil x = 120⁰ f'(120⁰) = -4 sin 2(120⁰) f'(120⁰) = -4 sin 240⁰ f'(120⁰) = -4(-√3/2) f'(120⁰) = 2√3 Karena f'(120⁰) < 0, maka fungsi f(x) naik pada interval 90⁰<x<180⁰ Jadi, fungsi naik pada interval 90°<x<180° Oleh karena itu, jawaban yang tepat adalah E. Semoga membantu yaa :)
· 0.0 (0)
Iklan
RR
R. Rahmatika
06 Januari 2022 09:41
Halo Winda, terimaksih sudah bertanya di Roboguru. Kakak akan bantu jawab ya Soal yang kamu tanyakan materinya tentang aplikasi turunan fungsi trigonometri ya. Perlu di ingat bahwa suatu fungsi f(x) akan naik pada saat f'(x)>0 Diketahui: f(x) = 2 cos 2x , pada interval 0⁰≤x≤180⁰ Maka, f'(x) = 2 (-sin 2x) (2) f'(x) = -4 sin 2x -4 sin 2x = 0 sin 2x = 0 sin 2x = sin 0⁰ 2x = 0⁰ + k.180⁰ x = 0⁰ + k. 90⁰ Saat k=0, maka x = 0⁰ Saat k=1, maka x = 90⁰ Saat k=2, maka x = 180⁰ Untuk mengetahui interval naik, Kamu harus melakukan Uji titik Misal x = 60 ( titik tersebut berada di antara 0⁰ dan 90⁰) Maka, f'(60⁰) = -4 sin 2(60⁰) f'(60⁰) = -4 sin 120⁰ f'(60⁰) = -4(√3/2) < 0 (fungsi turun pada interval 0⁰≤x≤90⁰) Misal x = 120⁰ ( titik tersebut berada di antara 90⁰ dan 180⁰) Maka, f'(120⁰) = -4 sin 2(120⁰) f'(120⁰) = -4 sin 240⁰ f'(120⁰) = -4(-√3/2) > 0 (fungsi naik pada interval 90⁰≤x≤180⁰) Jadi, fungsi naik pada interval 90⁰≤x≤180⁰ Jawaban E Saya akan lampirkan gambar grafik fungsi f(x) = 2 cos 2x , Agar kamu bisa lebih memahami maksud darj interval naik ya
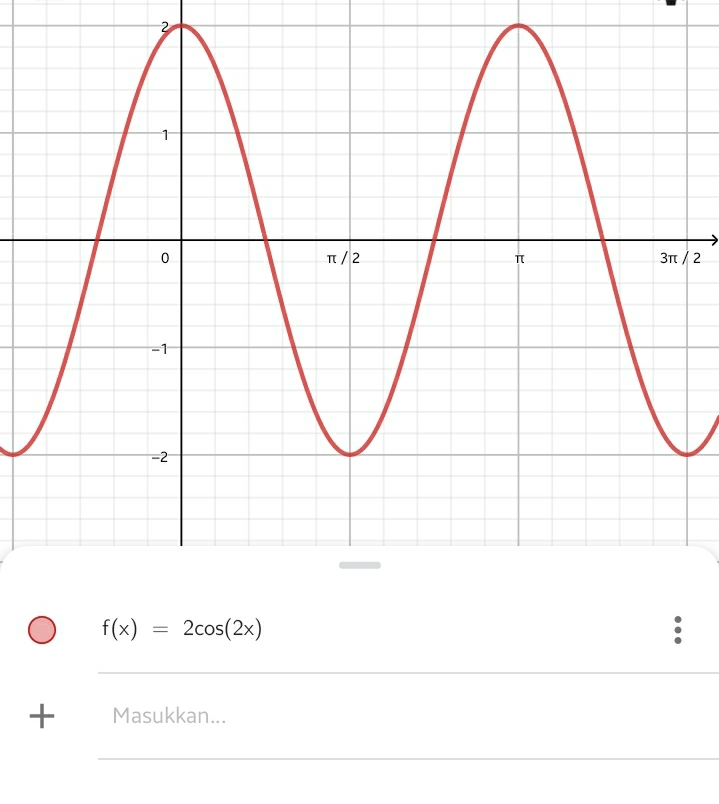
· 0.0 (0)
Mau pemahaman lebih dalam untuk soal ini?
Tanya ke AiRIS
Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

LATIHAN SOAL GRATIS!
Drill Soal
Latihan soal sesuai topik yang kamu mau untuk persiapan ujian


Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!



